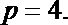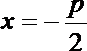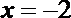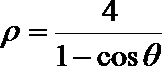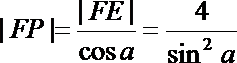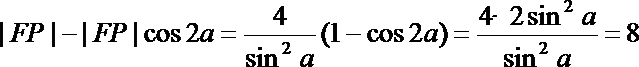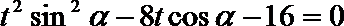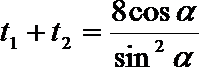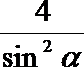圆锥曲线与方程_章节学习

1

题型：填空题

|

填空题 · 4 分

15．已知抛物线上一定点和两动点当是,点的横坐标的取值范围是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：填空题

|

填空题 · 4 分

2．抛物线的焦点坐标是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：简答题

|

简答题 · 14 分

19．已知抛物线的顶点为原点，其焦点到直线:的距离为．

（Ⅰ）求抛物线的方程;

（Ⅱ）设点为直线上一动点，过点作抛物线的两条切线,其中为切点，求直线的方程，并证明直线过定点．

（Ⅲ）过（Ⅱ）中的点的直线交抛物线于两点，过点分别作抛物线的切线，求交点满足的轨迹方程．

正确答案

（Ⅰ）

（Ⅱ）直线：定点

（Ⅲ）点满足的轨迹方程：

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：填空题

|

填空题 · 5 分

11.直线与抛物线围成的图形的面积等于______.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：简答题

|

简答题 · 14 分

20．如图，已知抛物线：和⊙：，过抛物线上一点作两条直线与⊙相切于、两点，分别交抛物线为E、F两点，圆心点到抛物线准线的距离为．

（1）求抛物线的方程；

（2）当的角平分线垂直轴时，求直线的斜率；

（3）若直线在轴上的截距为，求的最小值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：单选题

|

单选题 · 5 分

6. 若动圆的圆心在抛物线上，且与直线相切，则此圆恒过定点（）

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：简答题

|

简答题 · 13 分

20．如图，是抛物线为上的一点，弦SC，SD分别交x轴于A，B两点，且SA=SB。

（1）求证：直线CD的斜率为定值；

（2）延长DC交x轴于点E，若，求的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：简答题

|

简答题 · 13 分

16．已知点，直线，动点到点的距离等于它到直线的距离.

（Ⅰ）试判断点的轨迹的形状，并写出其方程.

（Ⅱ）是否存在过的直线，使得直线被截得的弦恰好被点所平分？

正确答案

（Ⅰ）因点到点的距离等于它到直线的距离，

所以点的轨迹是以为焦点、直线为准线的抛物线，其方程为.

（Ⅱ）解法一：假设存在满足题设的直线.设直线与轨迹交于，

依题意，得.

①当直线的斜率不存在时，不合题意.

②当直线的斜率存在时，设直线的方程为，

联立方程组，

消去，得，（*）

∴，解得.

此时，方程（*）为，其判别式大于零，

∴存在满足题设的直线　　　　　　　　　　

且直线的方程为：即. 　　

解法二：假设存在满足题设的直线.设直线与轨迹交于，

依题意，得.

易判断直线不可能垂直轴，

∴设直线的方程为，

联立方程组，

消去，得，

∵,

∴直线与轨迹必相交.

又，∴.

∴存在满足题设的直线　　　　　

且直线的方程为：即.

解法三：假设存在满足题设的直线.设直线与轨迹交于，

依题意，得.

∵在轨迹上，

∴有，将，得.

当时，弦的中点不是，不合题意，

∴，即直线的斜率,

注意到点在曲线的张口内（或：经检验，直线与轨迹相交）

∴存在满足题设的直线　

且直线的方程为：即.

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用直线与抛物线的位置关系圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 12 分

21.已知抛物线在x轴的正半轴上，过M的直线与C相交于A、B两点，O为坐标原点。

（I）若m=1，且直线的斜率为1，求以AB为直径的圆的方程；

（II）问是否存在定点M，不论直线绕点M如何转动，使得恒为定值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：单选题

|

单选题 · 5 分

9.已知直线过抛物线：的焦点，且与y轴垂直，则直线与抛物线所围成的图形的面积为（）

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：填空题

|

填空题 · 4 分

7．已知为抛物线上一点，设到准线的距离为，到点的距离为，则的最小值为________．

正确答案

4

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：填空题

|

填空题 · 5 分

15．已知点Ｆ为抛物线的焦点，O为原点，点Ｐ是抛物线准线上一动点，Ａ在抛物线上，且=4，则＋的最小值是__________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：单选题

|

单选题 · 5 分

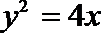
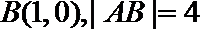
6．已知点A是抛物线上的点，点，则点A的横坐标为（）

A1

B2

C3

D4

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：简答题

|

简答题 · 12 分

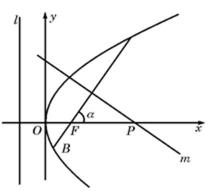
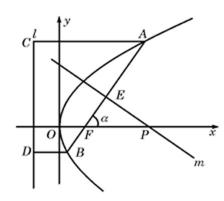
22．如图，倾斜角为α的直线经过抛物线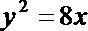的焦点F，且与抛物线交于A、B两点。

（1）求抛物线的焦点F的坐标及准线l的方程；

（2）若α为锐角，作线段AB的垂直平分线m交x轴于点P，证明|FP|-|FP|cos2α为定值，并求此定值

正确答案

（1）

解：设抛物线的标准方程为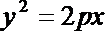，则，从而

因此焦点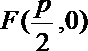的坐标为（2，0）.

又准线方程的一般式为

从而所求准线l的方程为

（2）解法一：如图（21）图作AC⊥l，BD⊥l，垂足为C、D，以F点为极点，F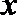为极轴建立极坐标系

则由抛物线的定义知抛物线方程为

则，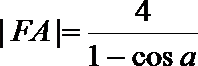

。

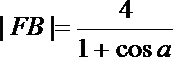
记直线m与AB的交点为E，则

所以

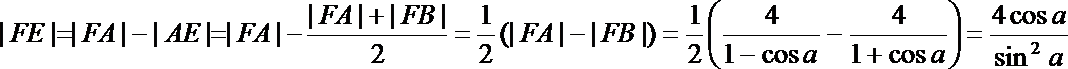
故

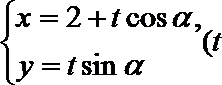
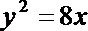
解法二：设直线AB：为参数）代入,得

因为直线AB与抛物线有两个交点，因此上述方程有两个根，设两个根分别为 t1，t2，

则

所以|FE|=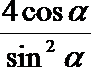, |FP|=

从而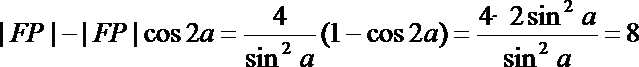为定值。

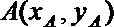
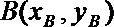
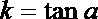
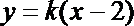
解法三：设，，直线AB的斜率为，则直线方程为。

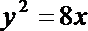
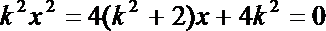
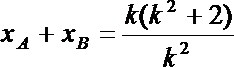
将此式代入,得，故。

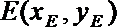
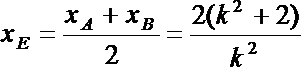
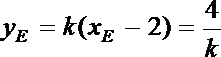
记直线m与AB的交点为，则

，

故直线m的方程为.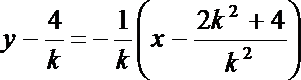

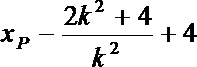
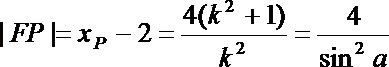
令y=0,得P的横坐标故

。

从而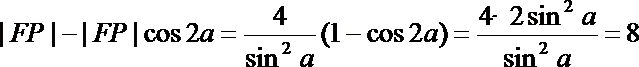为定值。

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

1

题型：填空题

|

填空题 · 5 分

14.过的直线交抛物线于、两点，则________。

正确答案

0

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点