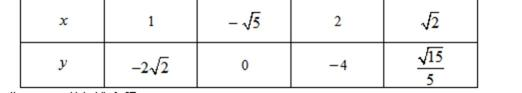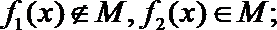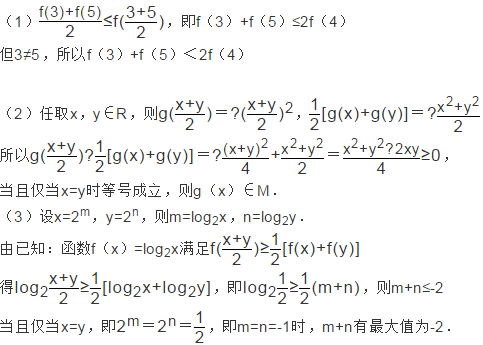- 圆锥曲线与方程
- 共2626题
4.抛物线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆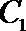
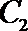

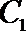

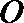
(1)求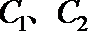
(2)过曲线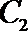
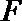
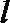
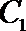
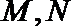
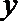
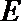
若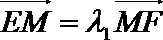
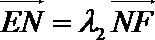
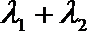
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知抛物线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知抛物线
(1) 






(2) 请你给出一个以

正确答案
(1) 设


(2) ① 研究


② 研究四边形


③ 研究五边形

④ 研究



⑤ 研究



⑥研究



解析
解析已在路上飞奔,马上就到!
知识点
14. 已知抛物线C的顶点在坐标原点,焦点为F(1,0),直线l与抛物线C相交于A、B两点.若AB的中点为(2,2),则直线l的方程为________.
正确答案
y=x
解析
解析已在路上飞奔,马上就到!
知识点
16.设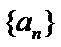
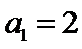
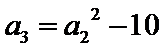
(Ⅰ)求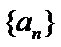
(Ⅱ)设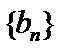
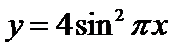
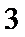
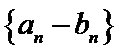
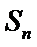
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.一青蛙从点





(1)若点





(2)若点




(3)若点




正确答案
(1)设
所以

(2) 依题意,
随着

(方法二)∴



又
∴
于是,当
当
∴
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知焦点在





(1)求椭圆
(2)已知过点




① 若直线


② 若直线




正确答案
(1)设椭圆


由题意可知:

解得
∴ 椭圆

(2)由(1)得

①当直线



由

即


则直线



∵ 

∴ 
②当直线



由


因为 点


因为 


所以

∴ 





取



记点

另一方面,点

∴点

又
故

所以 当直线



解析
解析已在路上飞奔,马上就到!
知识点
9.已知圆C过点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.定义在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.我们将具有下列性质的所有函数组成集合M:函数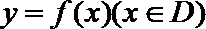
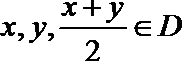

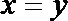
(1)若定义在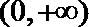
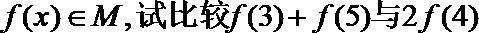
(2)给定两个函数: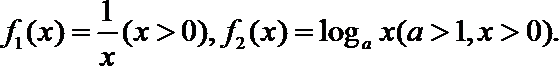
(3)试利用(2)的结论解决下列问题:若实数m,n满足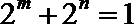
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
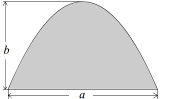
13.如图所示,已知抛物线拱形的底边弦长为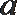
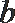
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25.已知抛物线














(

(


(




正确答案
(





四边形

设直线


解得
伴随直线的解析式为

(


伴随四边形的面积为

故

即抛物线的解析式可能是




抛物线的解析式还可能是




(


伴随直线是

设


∴



当


当

抛物线的解析式为



即
即
故

解析
解析已在路上飞奔,马上就到!
知识点
5.若抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析