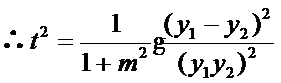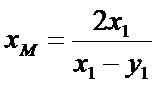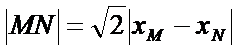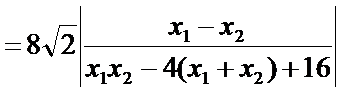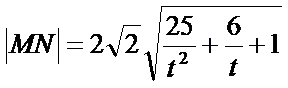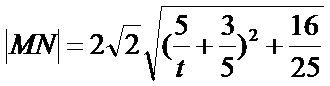- 圆锥曲线与方程
- 共2626题
12.过抛物线






正确答案
解析
设








考查方向
解题思路
先通过焦半径, 算出直线AB的倾斜角, 再利用数形结合的方法, 计算顶点到直线AB的距离
易错点
忽略AB是焦点弦, 找不到恰当的解题方法
知识点
14.已知抛物线





正确答案
2
解析
如图,由题意可得 AF=AC设AF=3m,由AB=2BC,可AB=2m,BC=m,过A作AD垂直x轴于D,设A的横坐标为


考查方向
解题思路
画出抛物线简图,用抛物线定义,结合题中的位置关系,数量关系,求出点A(2,2
易错点
对抛物线定义及性质掌握不熟
知识点
.
23.求抛物线
24.已知动圆







正确答案
(1)
解析
(1) 设抛物线的焦点为

由







考查方向
解题思路
联立直线与抛物线方程,求解抛物线过焦点的弦长.
设动圆圆心

易错点
联立消元计算出错
第2问计算量较大,对学生的运算能力是个严重的考验。
不能正确地两次利用基本不等式求最值。
正确答案
(2)
解析
设动圆圆心

且圆
令

解得:
设
当

当





综上①知



当且仅当

所以

考查方向
解题思路
联立直线与抛物线方程,求解抛物线过焦点的弦长.
设动圆圆心

易错点
联立消元计算出错
第2问计算量较大,对学生的运算能力是个严重的考验。
不能正确地两次利用基本不等式求最值。
14.如图,探照灯反射镜的纵截面是抛物线的一部分,光源在抛物线的焦点F处,灯口直径AB为



正确答案


解析
.建立如图平面直角坐标系,设抛物线方程为
则点A(40,30)在抛物线上, 

考查方向
解题思路
1.建立平面直角坐标系设出抛物线的方程;
2.根据题意点A(40,30)在抛物线上求出p;
易错点
不会将题中给出的应用问题建立坐标系求解;
知识点
已知




24.求

25.如图5所示,过


(点



正确答案
(1)

解析
(Ⅰ)由点




抛物线的方程为


考查方向
解题思路
1.先利用抛物线定义求出p,然后将点M的坐标带入求解即可;2.设出直线



易错点
不会利用抛物线的定义转化题中的条件



正确答案
(2)略
解析
(Ⅱ):显然直线

分别设


联立

联立

设



则


故

注意到点


故得



考查方向
解题思路
1.先利用抛物线定义求出p,然后将点M的坐标带入求解即可;2.设出直线



易错点
1.不会利用抛物线的定义转化题中的条件



设抛物线









正确答案
解析
如图,由









考查方向
解题思路
1、由直线







易错点
本题难在定义的应用和几何关系的寻找。
知识点
已知抛物线


23.求抛物线C的方程;
24.已知动圆P的圆心在抛物线C上,且过定点D(0,4),若动圆P与x轴交于A、B两点,且

正确答案
(Ⅰ)
解析
(1) 设抛物线的焦点为

由








考查方向
解题思路
过抛物线焦点的弦长运用抛物线的定义可求得;求出
易错点
本题抛物线为开口向上的,故焦点弦长为

正确答案

解析
设动圆圆心

且圆
令

解得:

当

当




所以

考查方向
解题思路
过抛物线焦点的弦长运用抛物线的定义可求得;求出
易错点
本题抛物线为开口向上的,故焦点弦长为

动点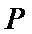
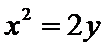
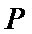

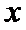
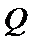
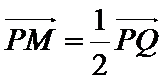
23.求点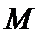
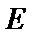
24.设点




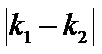
正确答案
详见解析
解析
解:(Ⅰ)设点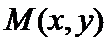
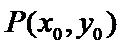
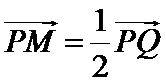
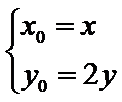
因为点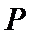

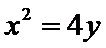
考查方向
求圆锥曲线的轨迹方程
解题思路
设参数,找等量关系,求解参数
易错点
计算能力弱,数形结合思想运用不牢
教师点评
解析几何一般都需要学生拥有一个强大的计算能力
正确答案
详见解析
解析
(Ⅱ)由已知,直线的斜率一定存在,
设点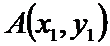
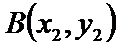
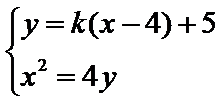
得,
由韦达定理,得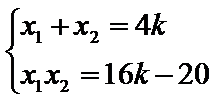
当直线经过点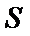
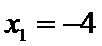

当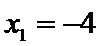
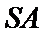
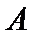
则 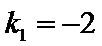

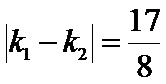
同理,当点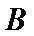
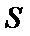

直线不经过点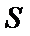
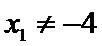

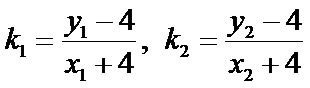


故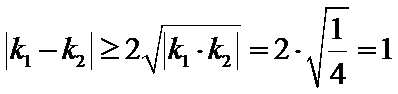
所以
考查方向
抛物线的性质及应用,直线和圆锥曲线的交汇问题 直线的斜率,求圆锥曲线的轨迹方程
解题思路
设出相关点的坐标,利用直线和圆锥曲线的方程联立,带入坐标,求解参数的值,利用平均值不等式判断求解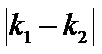
易错点
计算能力弱,不会用平均值不等式求最值
已知抛物线C的标准方程为

23.求抛物线C的标准方程;
24.记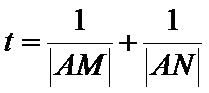
正确答案
抛物线C的标准方程为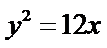
解析
由题意,

抛物线C的标准方程为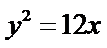
考查方向
求抛物线的标准方程,圆锥曲线和直线的交汇问题
解题思路
根据三角形的面积公式,抛物线的几何性质,建立关于p的方程,然后求出p
易错点
抛物线的几何性质掌握不好,计算求解错误
教师点评
主要是找到等量关系,建立方程,进而求出p
正确答案
不论a取何值,t均与m有关, 即
仅当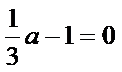

解析
设
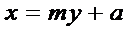
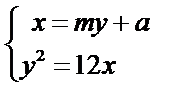

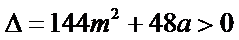
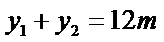


(ⅰ)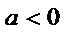


又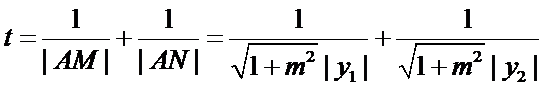
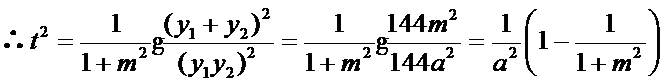
不论a取何值,t均与m有关, 即
(ⅱ)





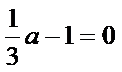

考查方向
求抛物线的标准方程,圆锥曲线和直线的交汇问题
解题思路
设出相关变量的参数,然后联立成方程组,利用代数方法解决几何问题。
在讨论a时,要对a的符号进行讨论,最后结合讨论结果,给出答案。
教师点评
本题主要难在计算量上,在设参数然后“解析”的时候,要注意运算正确


正确答案
解析
二项式


知识点
正确答案
知识点
5.抛物线


正确答案
解析
依题意可知抛物线的准线方程为
∴点A到准线的距离为4+1=5,
根据抛物线的定义可知点A与抛物线焦点的距离就是点A与抛物线准线的距离,
∴点A与抛物线焦点的距离为5,
故选A.
考查方向
解题思路
先根据抛物线的方程求得准线的方程,进而利用点A的纵坐标求得点A到准线的距离,进而根据抛物线的定义求得答案.
易错点
圆锥曲线的定义要熟练的掌握并学会灵活应用.
知识点
定期存款较股票型基金产品有一定特点,下列说法正确的是( )。
A.流动性高;收益率高
B.流动性高;收益率低
C.流动性低;收益率低
D.流动性低;收益率高
正确答案
C
解析
[解析] 一般说来,定期存款低于股票型基金产品的收益率,流动性也低于股票型基金产品。
已知抛物线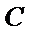
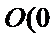
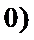
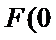
23.求抛物
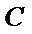
24.过点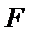
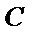
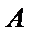
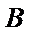
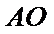
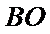
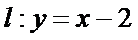
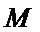
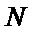
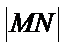
正确答案
解:由题意,设抛物线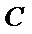
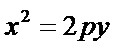
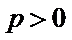
则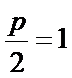
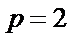
所以抛物线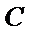
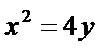
解析
解:由题意,设抛物线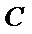
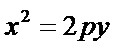
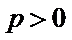
则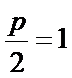
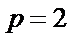
所以抛物线
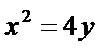
考查方向
抛物线的标准方程
解题思路
熟练掌握抛物线的四种形式即可求解。
易错点
容易把抛物线的对称轴弄反了。
教师点评
熟记抛物线的标准方程是关键。
正确答案
解:由题意,直线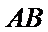
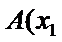
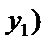
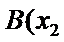
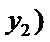
直线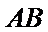
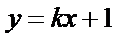
由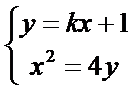
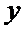
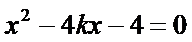
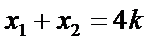
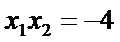
从而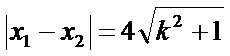

由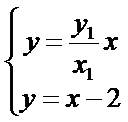
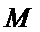
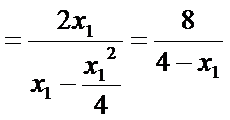
同理点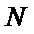
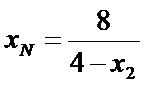
所以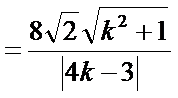
令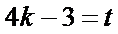
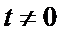
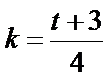
当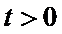
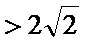
当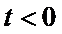
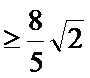
综上所述,当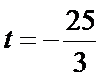
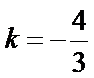
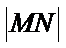
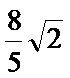
解析
解:由题意,直线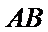
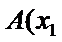
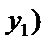
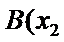
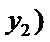
直线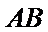
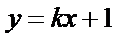
由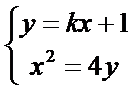
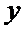
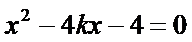
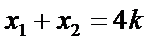
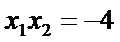
从而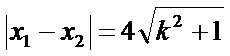

由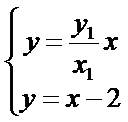
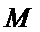
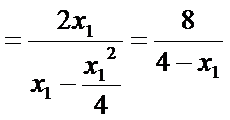
同理点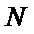
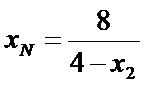
所以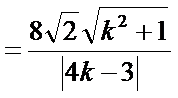
令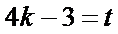
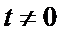
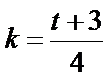
当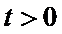
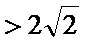
当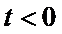
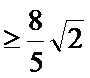
综上所述,当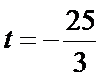
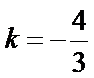
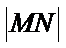
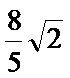
考查方向
弦长公式及最值问题。
解题思路
联立直线和抛物线的方程,然后用韦达定理的两根的关系,再同弦长公式表示出来,最后配方得到最小值。
易错点
1、解方程出错;2、将弦长公式表示出来后,没有思路。
教师点评
本题考查了抛物线的标准方程及直线与抛物线的位置关系,弦长公式、最值问题。
14.若抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析