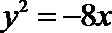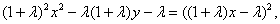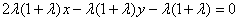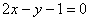- 圆锥曲线与方程
- 共2626题
4.已知一个空间几何体的三视图如右图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
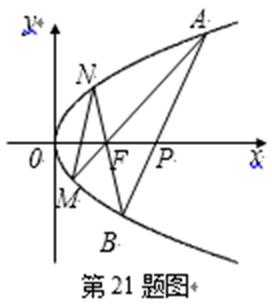
21.如图,已知抛物线






(1)证明
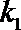


(2)记直线
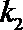

正确答案
证明:(1)依题意,设直线

将其代入

整理得 
从而
于是
∴

又
(2)证明:设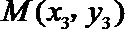
则 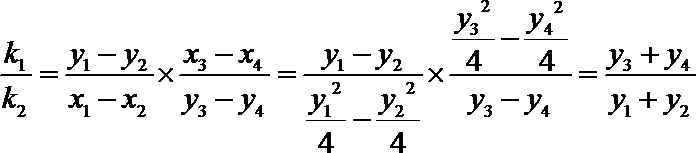
设直线

将其代入

整理得
∴
同理可得 
故
由(1)知,
∴
解析
解析已在路上飞奔,马上就到!
知识点
7.已知点









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知斜率为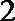
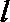
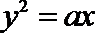
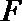
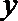
正确答案
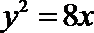
解析
解析已在路上飞奔,马上就到!
知识点
9.直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.抛物线y=x2与直线x-y+2=0构成封闭平面区域(含边界)为D.若曲线x2-2ax+y2-4y+a2+ 
正确答案
解析
曲线
即为
其圆心坐标为E(a,2),半径
由图可知,当
圆与点D有公共点;
当a<0时,要圆与点D有公共点,
只需圆心到直线l:x-y+2=0的距离
则a的最小值为-
知识点
6.直线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知点




(Ⅰ)试判断点

(Ⅱ)是否存在过




正确答案
(Ⅰ)因点


所以点




(Ⅱ)解法一:假设存在满足题设的直线



依题意,得
①当直线
②当直线


联立方程组
消去

∴

此时,方程(*)为
∴存在满足题设的直线
且直线


解法二:假设存在满足题设的直线



依题意,得
易判断直线

∴设直线

联立方程组
消去

∵
∴直线与轨迹
又

∴存在满足题设的直线
且直线


解法三:假设存在满足题设的直线



依题意,得
∵

∴有


当


∴


注意到点



∴存在满足题设的直线
且直线


解析
解析已在路上飞奔,马上就到!
知识点
5.过抛物线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.抛物线y=x2与直线x-y+2=0构成封闭平面区域(含边界)为D.若曲线x2-2ax+y2-4y+a2+ 
正确答案
解析
曲线
即为
其圆心坐标为E(a,2),半径
由图可知,当
圆与点D有公共点;
当a<0时,要圆与点D有公共点,
只需圆心到直线l:x-y+2=0的距离
则a的最小值为-
知识点
4.若直线,交抛物线C:y2=2px(p>0)于两不同
点A,B,且|AB|=3p,则线段AB中点M到
y轴距离的最小值为( )
正确答案
解析
由题意可得抛物线的准线l:
分别过A,B,M作AC⊥l,BD⊥l,MH⊥l,垂足分别为C,D,H。在直角梯形ABDC中,
由抛物线的定义可知AC=AF,BD=BF(F为抛物线的焦点)
即AB的中点M到抛物线的准线的最小距离为
∴线段AB中点M到y轴距离的最小值为
考查方向
抛物线的性质与特征
解题思路
分别过A,B,M作AC⊥l,BD⊥l,MH⊥l,垂足分别为C,D,H,要求M到y轴的最小距离,只要先由抛物线的定义求M到抛物线的准线的最小距离d,即可求解.
易错点
对图像的性质掌握不牢固,不会应用转化思想解题
教师点评
本题考查线段中点到y轴距离的最小值的求法,解题时要认真审题,注意抛物线性质的合理运用
知识点
10.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若

则|QF|=( )
正确答案
解析
试题分析:
如图,设






又
故选B.
考查方向
解题思路
本题考查了抛物线的简单性质,需要先得到比例关系,再用抛物线定义转化,得出结果
易错点
本题在比例转化过程中易错。
知识点
设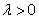
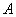

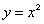
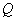
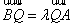
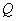
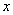
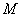
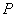
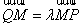
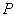
正确答案
P的轨迹方程为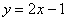
解析
本题考查直线和抛物线的方程,平面向量的概念,性质与运算,动点的轨迹方程等基本知识,考查灵活运用知识探究问题和解决问题的能力,全面考核综合数学素养。
由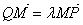
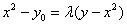

再设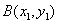

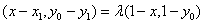

将①式代入②式,消去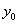
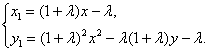
又点B在抛物线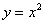
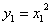
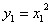
整理得
因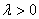
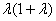
故所求点P的轨迹方程为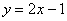
知识点
如图,已知两条抛物线










(1) 证明:
(2)过原点








正确答案
见解析。
解析
本题以二次曲线中的抛物线和直线相关知识为背景,考察学生的运算和推演能力,考查转化化归思想的运用。
(1)设直线l1:y=kx,l2:y=mx(k≠m,k≠0,m≠0)分别代入E1,E2的方程得
A1



一是当k=-m时,直线A1B1与A2B2的斜率都不存在,A1B1‖A2B2;
二是当k

综合可见,A1B1‖A2B2。
(2)设直线l:y=nx,则C1


另一法:由(1)知,两个三角形三边对应平行,它们相似。面积比为边的比的平方。可得。
知识点
扫码查看完整答案与解析