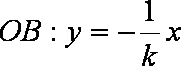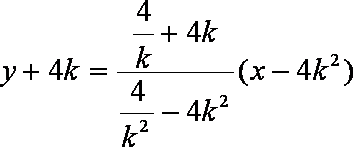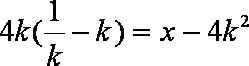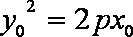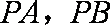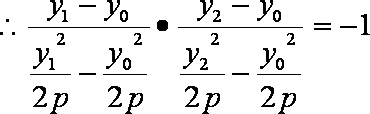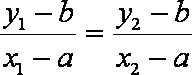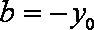- 圆锥曲线与方程
- 共2626题
选修4-4:坐标系与参数方程
在极坐标系中,过点

(1)将

(2)在极坐标系中,以极点为坐标原点,以极轴为
若曲线






正确答案
见解析。
解析
(1)画图可知
(2)直线



知识点
在直角坐标平面内,将每个点绕原点按逆时针方向旋转





(1)求矩阵

(2)求曲线


正确答案
(1)
解析
(1)在直角坐标平面内,将每个点绕原点按逆时针方向旋转


(2)将每个点横、纵坐标分别变为原来的







(1)


(2)




故所求的曲线方程为:
知识点
在直角坐标平面内,以坐标原点






(1)分别求出曲线

(2)若点




正确答案
(1)

解析
(1)由曲线






(2)由圆心(2,0)到直线




(1)由







即
(2)因为圆心







知识点
选修4-4:坐标系与参数方程
已知曲线C1:


(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线




正确答案
见解析。
解析
(1)







因为圆心


所以

(2)压缩后的参数方程分别为





化为普通方程为:



联立消元得
其判别式
所以压缩后的直线



知识点
选修4—2:矩阵与变换
设矩阵
(1)若

(2)若曲线C:


求
正确答案
见解析。
解析
(1)当

(2)设曲线C上任意一点


又点



即
又已知曲线C的方程为
比较系数可得


知识点
选修4—4:极坐标与参数方程
在直角坐标平面内,以坐标原点






(1)分别求出曲线

(2)若点




正确答案
见解析。
解析
(1)由







即
(2)因为圆心







知识点
已知动点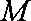
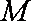
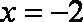
(1)求点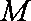
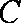
(2)大家知道,过圆上任意一点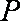
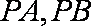
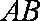
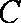
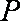
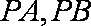
(ⅰ)若点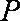
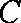
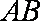
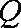
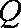
(ⅱ)试探究:若改变曲线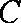
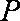
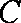
正确答案
见解析。
解析
(1)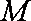
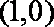
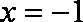
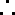
轨迹方程为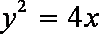
(2)(i)依题意得设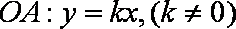
由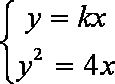
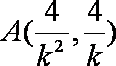
同理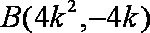
因此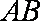
即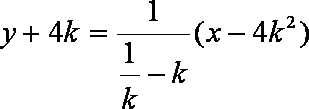
令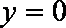
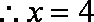
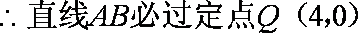
(ii)结论:过抛物线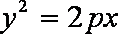
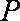
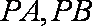
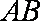
设点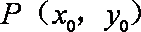
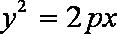
过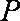
设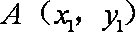
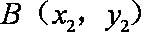
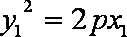
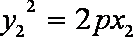
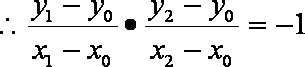
化简得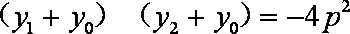
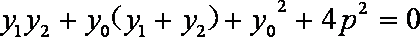
假设
即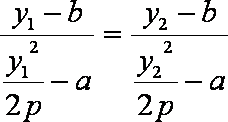
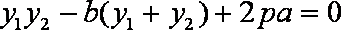
比较(*)、(**)得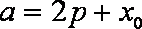
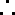
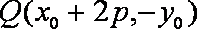
(如用其它方法,请对照给分)
知识点
已知圆C1的方程为

(1)求动圆圆心C的轨迹M的方程;
(2)斜率为k的直线l与轨迹M相切于第一象限的点P,过点P作直线l的垂线恰好经过点A(0,6),并交轨迹M于异于点P的点Q,记

正确答案
见解析
解析
解(1)设动圆圆心C的坐标为

可得 
由于圆C1在直线l的上方,所以动圆C的圆心C应该在直线l的上方,所以有


(2)如图示,设点P的坐标为







把直线PQ的方程与轨迹M的方程联立得



知识点
选修4-2:矩阵与变换
若点




(2)求曲线C:x2+y2=1在矩阵N=
正确答案
见解析。
解析
法一:



即M=




法二:同法一可求得M=






(2)
知识点
如图,在圆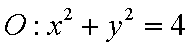
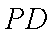
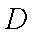
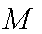
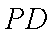
(1)当点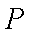

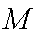
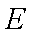
(2)若圆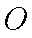
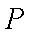
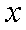
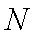


正确答案
(1)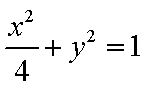
解析
(1)由于点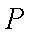

(2)由(1)得到轨迹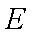


(1)设
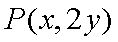

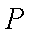


即点
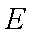

(2)解法一:
(i) 当直线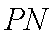


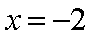
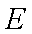
(2)当直线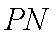

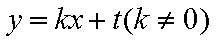
因为直线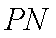

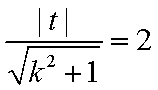
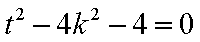
又直线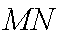
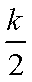
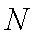
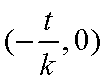
所以直线
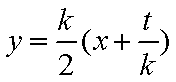
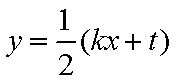
由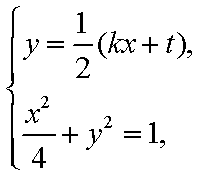
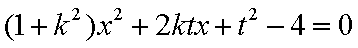
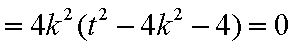

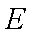
综上(i)(2)知,直线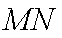
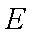
解法二 :设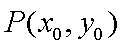

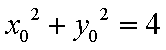
(i)当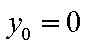


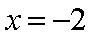


(2)当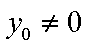

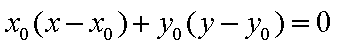
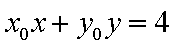
令
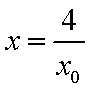
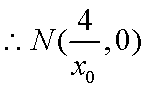
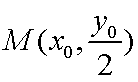
所以直线
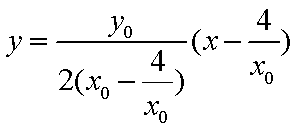

由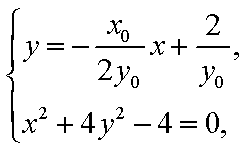

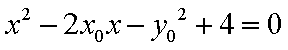
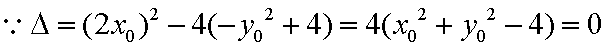

综上(i)(2)知,直线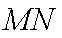

知识点
11.已知曲线

正确答案

解析
分焦点在x轴和y轴上两种情况,
当焦点在x轴上时,

当焦点在y轴上时,

知识点
13.能够把圆






上述函数不是圆
正确答案
③
解析
若为和谐函数,则该函数为过原点的奇函数,显然①②④都满足条件,而③不是奇函数,所以不是圆O的和谐函数,所以答案为③。
知识点
3.曲线
正确答案
解析
当





当





知识点
已知





(1)求点P的轨迹方程;
(2)是否存在定直线

正确答案
见解析。
解析
(1)设B(0,t),设Q(m,0),t2=


















(2)由(1),点P的轨迹方程是y2=x;设P(y2,y),


L=2
=2

若a为常数,则对于任意实数y,L为定值的条件是a-





知识点
20.已知动圆












(1)求曲线
(2)试探究

(3)记





正确答案
见解析。
解析
(1)设圆心

由于动圆


圆





故圆心

(2)设

由

由


(3)




令







知识点
扫码查看完整答案与解析