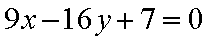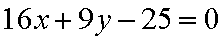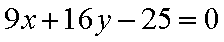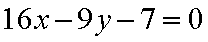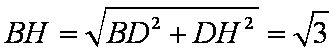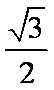- 圆锥曲线与方程
- 共2626题
在椭圆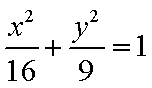
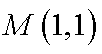
正确答案
解析
略
知识点
已知椭圆C: 

(1)求椭圆C的方程;
(2)若斜率为k的直线过点M(2,0),且与椭圆C相交于A, B两点.试探讨k为何值时,三角形OAB为直角三角形.
正确答案
(1)
(2)
解析
(1)

(2)由已知直线AB的斜率存在,设AB的方程为:
由
,得:
设
1)若





2)若





解得,


知识点
椭圆C:

(1)求椭圆C的方程;
(2)设椭圆C的左,右顶点分别为A,B ,点P是直线
正确答案
见解析
解析
解析:
(1)依题意
过焦点F与长轴垂直的直线x=c与椭圆
联立解答弦长为
所以椭圆的方程
(2)设P(1,t)


即
可知

则
同理得到
由椭圆的对称性可知这样的定点在
不妨设这个定点为Q
又





知识点
抛物线C1:



(1)求椭圆C2的标准方程;
(2)过A点作直线







正确答案
见解析
解析
(1)∵


又∵

代入抛物线方程得

∴椭圆C2的标准方程为
(2)设直线


设
又因为
直线



由

所以
则
所以
所以


知识点
已知椭圆C


不同的点P,使得△F1F2P为等腰三角形,则椭圆C的离心率的取值范围是
正确答案
解析
略
知识点
已知椭圆



(1)求椭圆
(2)设








(3)在(2)的条件下,过点



正确答案
见解析
解析
解析:(1)由题意知
而以原点为圆心,椭圆短半轴为半径的圆的方程为
故由题意可知
故椭圆C的方程为
(2)由题意知直线

由
设点



令


得
由①得
代入②整得,得
(3)①当过点


解得

② 当过点

设直线



由

计算得,
则
因为


所以

知识点
已知椭圆C:

(1)若椭圆的长轴长为4,离心率为
(2)在(1)的条件下,设过定点






(3)如图,过原点








正确答案
见解析
解析
(1)
(2)显然直线x=0不满足题设条件,可设直线l:
由


由

得
(3)由椭圆的对称性可知PQSR是菱形,原点O到各边的距离相等。
当P在y轴上,Q在x轴上时,直线PQ的方程为
由d=1得
当P不在y轴上时,设直线PS的斜率为k,

由,得

在Rt△OPQ中,由
所以



知识点
已知F1(-1,0),F2(1,0)为椭圆C的左、右焦点,且点P(1,
(1)求椭圆C的方程;
(2)过点F1的直线l交椭圆C于A,B两点,问△F2AB的内切圆的面积是否存在最大值?若存在求其最大值及此时的直线方程;若不存在,请说明理由。
正确答案
见解析
解析
解析:(1)由已知,可设椭圆

因为


所以,椭圆
(也可用待定系数法

………………4分
(2)当直线




设


所以
设内切圆半径为





令


又当


故当


………………12分
知识点
已知椭圆



(1)求椭圆
(2)设直线






正确答案
见解析
解析
解析:(1)由已知,

又点


由①②解之,得
故椭圆

(2) 当直线

则由
消去


设A、B、


由于点


从而

又点



当直线


从而





所以点

知识点
已知椭圆





(1)求该椭圆的标准方程;
(2)当点













正确答案
见解析
解析
(1)由










故椭圆的标准方程为 
(2)设

则


动点


由
设



因为点


故
所以







知识点
已知椭圆E:
原点对称的两点,且直线PA的斜率与直线QA的斜率之积为
(1)求E的方程;
(2)过E的右焦点作直线与E交于M、N两点,直线MA、NA与直线
分别交于C、D两点,设△ACD与△AMN的面积分别记为


正确答案
见解析
解析
(1)设

又
故
(2)设直线


设
直线MA的方程为

同理
所以
所以



所以
记

所以


故
知识点
已知椭圆


(1)求椭圆
(2)若



试确定
正确答案
见解析。
解析
(1)由已知,


由




∴

(2)①若直线





②若直线


由

∴
∴
∵


综上,

知识点
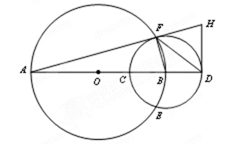
如图,已知AB为圆O的一条直径,以端点B为圆心的圆交直线AB于C、D两点,交圆O
于E、F两点,过点D作垂直于AD的直线,交直线AF于点H。
(1)求证:B、D、H、F四点共圆;
(2)若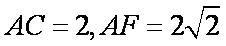
正确答案
见解析
解析
(1)因为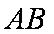
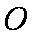
又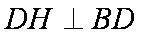
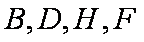
(2)因为AH与圆B相切于点F,
由切割线定理得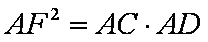
所以
又△AFB∽△ADH,所以
由此得
连接BH,由(1)知,BH为△BDF外接
故△BDF的外接圆半径为
知识点
极坐标系中椭圆C的方程为 

(1)求该椭圆的直角标方程,若椭圆上任一点坐标为

(2)若椭圆的两条弦




正确答案
见解析。
解析
(1)该椭圆的直角标方程为
设
所以

(2)设直线



则直线


代入
即
设


同理
所以
知识点
如图,已知椭圆



(1)求此椭圆的标准方程;
(2)设P此椭圆上异于A,B的任意一点, 






正确答案
见解析
解析
解析:(1)可知,




得
椭圆方程为
(2)设
由

所以直线AQ的方程为
由

由
又因为
所以
所以直线NQ的方程为
化简整理得到
所以点O直线NQ的距离
直线

知识点
扫码查看完整答案与解析