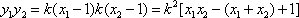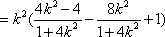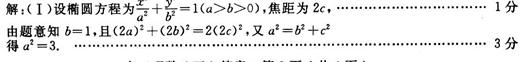- 圆锥曲线与方程
- 共2626题
已知椭圆C的中心在原点,一个焦点F(-2,),且长轴长与短轴长的比是2:
(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点,若当
正确答案
见解析。
解析
(1)设椭圆

由题意有:
解得
故椭圆

(2)设


因为
因为当




故有

又点

故实数

知识点
如图,椭圆 


交于M、N两点。
(1)求椭圆C的方程;
(2)求证△APB为直角三角形;
(3)设直线MN的斜率为n,求证: 
正确答案
见解析。
解析
知识点
已知椭圆C的中点在原点,焦点在


(1)求椭圆C的方程;
(2)已知点

正确答案
见解析。
解析
知识点
已知双曲线C:



( I )求椭圆E的方程;
(2)设点A是椭圆E的左顶点,P、Q为椭圆E上异于点A的两动点,若直线AP、AQ的斜率之积为
正确答案
见解析。
解析
知识点
已知椭圆




(1)求椭圆
(2)过右焦点















正确答案
见解析。
解析
(1)由条件知
故所求椭圆方程为
(2)设过点




将直线



整理得:
因为点


且
直线



令



直线

将

所以

知识点
已知椭圆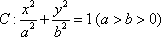


(1)求椭圆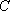
(2)直线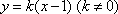
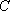

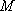

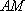
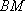



正确答案
见解析
解析
(1)由题意得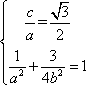
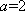
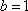
所以椭圆

(2)以线段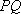

由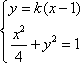

设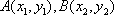
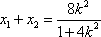

又因为点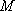

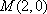
由题意可知直线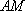
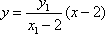
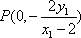
直线
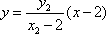
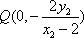
若以线段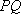

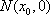

又因为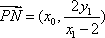
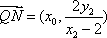
所以
又因为
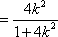
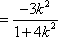
所以
解得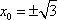
故以线段

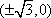
知识点
已知椭圆
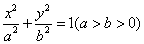


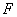
(1)求椭圆
(2)过点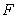
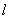
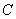
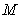
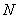

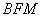
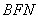
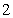
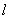
正确答案
见解析
解析
(1)由已知得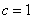

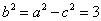

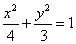
(2)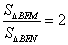
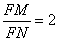
当直线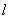

当直线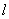

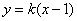
由
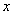
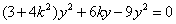
设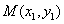
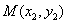

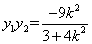
由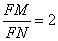
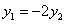
由①②③解得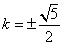
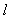
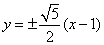
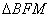
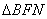
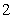
知识点
已知椭圆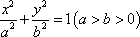
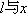
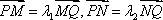
(1)求椭圆的标准方程;
(2)若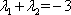
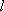
正确答案
见解析
解析
知识点
设椭圆




(1)求椭圆C的方程;
(2)抛物线










正确答案
见解析。
解析
知识点
已知椭圆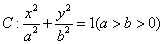
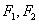
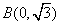
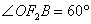
(1)求椭圆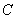
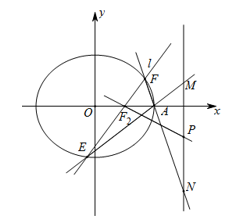
(2)如图,过右焦点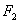
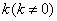
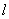
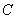
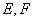
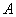
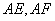
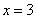
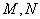
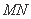
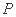
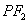
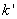
求证: 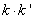
正确答案
见解析
解析
(1)由条件可知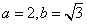
故所求椭圆方程为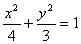
(2)设过点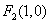
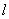
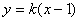
由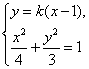
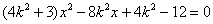
因为点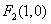
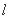
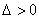
设点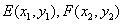
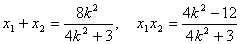
因为直线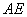
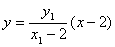
直线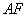
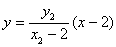
令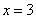
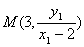
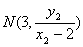
所以点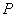
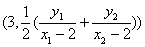
直线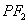
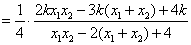
所以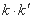
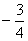
知识点
设

(1)设椭圆C上的点

(2)设K是(1)中所得椭圆上的动点,求线段
(3)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直
线PM ,PN的斜率都存在,并记为

直线L有关,并证明你的结论。
正确答案
见解析。
解析
(1)由于点
又2


焦点坐标分别为
(2)设

把




(3)过原点的直线L与椭圆相交的两点M,N关于坐标原点对称,
设



故:


知识点
椭圆






正确答案
解析
设交点分别为







知识点
已知双曲线

正确答案
解析
由题意知在双曲线中



知识点
以椭圆


(1)求椭圆C及其“准圆”的方程;
(2)若椭圆C的“准圆”的一个弦ED(不与坐标轴垂直)与椭圆C交于M、N两点,试证明:当
正确答案
见解析
解析
知识点
已知双曲线

(1)求椭圆标准方程;
(2)设动点P满足:

求证:存在定点


(3)若








正确答案
见解析。
解析
(1)解:由题设可知:双曲线

所以椭圆中的
又由椭圆的长轴为4得
故
故椭圆的标准方程为:
(2)证明:设

由直线OM与ON的斜率之积为

由①②可得:
M、N是椭圆上,故
故
由椭圆定义可知存在两个定点

(3)证明:设
由题设可知
由题设可知

将③代入④可得:




所以
因此以
知识点
扫码查看完整答案与解析