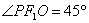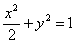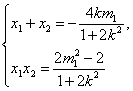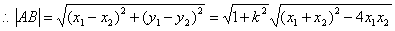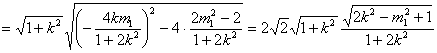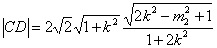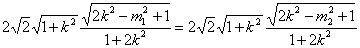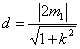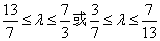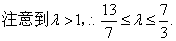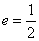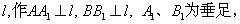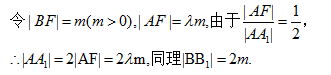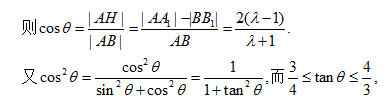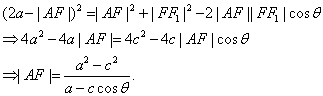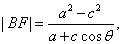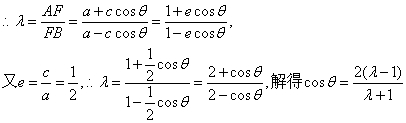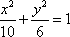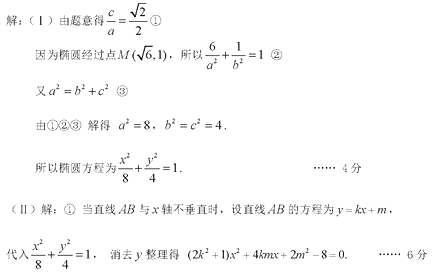- 圆锥曲线与方程
- 共2626题
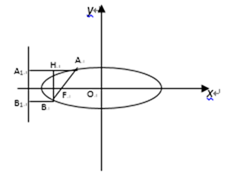
如图,椭圆






(1)求该椭圆的离心率;
(2)设线段











正确答案
(1)
(2)
解析
(1)解:依题意,当直线


设 
则 
将 

解得 
所以椭圆的离心率为 
(2)解:由(1),椭圆的方程可设为
设

依题意,直线





则 


………………8分
因为 
所以 

因为 △

所以 

所以

知识点
给定椭圆








(1)求椭圆
(2)点




(ⅰ)当点



(ⅱ)求证:线段
正确答案
见解析
解析
(1)


准圆方程为
(2)(ⅰ)因为准圆


设过点

所以由

因为直线
所以

所以



(ⅱ)①当直线

则

当



此时



同理可证当


②当


设经过点

所以由
得
由

因为

设


所以

所以

综合①②知:因为



所以线段


所以线段
知识点
已知椭圆


(1)求椭圆E的方程;
(2)设直线l:y=kx+t 与圆
①求证:
②当R为何值时,
正确答案
见解析
解析
(1) 椭圆E的方程为
(2) ①因为直线


即 

由

则

②由①②,得 





∴


∴
知识点
已知椭圆


(1)求椭圆
(2)若直线






正确答案
见解析
解析
(1)由题意椭圆的离心率


∴椭圆方程为
又点
∴椭圆的方程为
(2)设




所以






当


当

综上可知,直线
知识点
在直角坐标系xOy中,椭圆C1:


(1)求C1的方程;
(2)平面上的点N满足


正确答案
(1)椭圆
(2)直线

解析
(1)由


设




得






消去



故椭圆

(2)由


因为


故

设

由
消去

设



因为



所以

故所求直线


知识点
如图,已知椭圆E: 





(1)求椭圆E的方程;
(2)求证:点M在直线
(3)是否存在实数k,使得三角形BDM的面积是三角形ACM的3倍?若存在,求出k的值;若不存在,说明理由。
正确答案
见解析
解析
(1)由题意可知


所以,椭圆的标准方程为
(2)设




所以,


于是
因为


(3)由(2)知点A到直线CD的距离与点B到直线CD的距离相等,
若∆BDM的面积是∆ACM面积的3倍,
则|DM|=3|CM|,因为|OD|=|OC|,于是M为OC中点,;
设点C的坐标为



于是


知识点
已知椭圆

正确答案
①②③
解析
略
知识点
在平面直角坐标系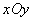
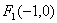
(1)求椭圆G的标准方程;
(2)已知直线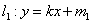
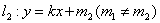
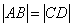
(i)证明: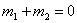
(ii)求四边形ABCD的面积S的最大值.
正确答案
见解析
解析
(1)设椭圆G的标准方程为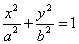
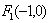
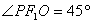
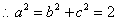

(2)设A(
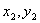
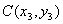
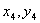
(i)证明:由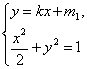
则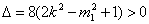
同理
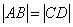
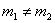
(ii)解:由题意得四边形ABCD是平行四边形,设两平行线AB,CD间的距离为d,则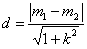
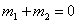
当且仅当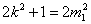
知识点
已知椭圆E:

(1)求椭圆E的方程;
(2)若点A与椭圆上的另一点C(非右顶点)关于直线l对称,直线l上一点N(0,y0)满足
正确答案
见解析
解析
知识点
如图;.已知椭圆C:





正确答案
见解析
解析
(1)由题意知


故椭圆C方程为
(2)点M与点N关于

不妨 设

由已知

由于



当




(3)假设存在满足条件的点P,设




故
又点M与点P在椭圆上,故
得





由P为椭圆上的一点,




知识点
已知直角




正确答案
解析
(法一)
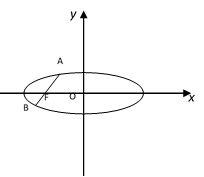
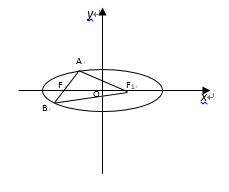
如图,不妨设




由题意可得方程组:
故有:

(法二)
如图,设
由椭圆的第二定义有
得:

(法三)
如图, 
在
由椭圆的性质可得:


知识点
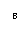
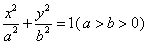

正确答案
见解析。
解析
解法1
由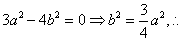
设AB的倾斜角为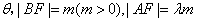
则
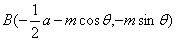
由于A、B两点在椭圆上,
∴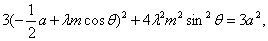
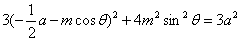
②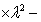
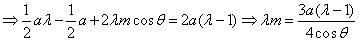
将③代入①得
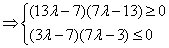
解法2
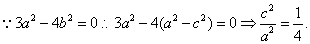
设椭圆对应于F的准线为
解法3
如图
角为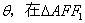
同理,在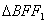
以下与解法2相同
知识点
已知椭圆的中心在原点
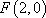
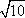
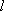
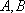
(1)求这个椭圆的标准方程;
(2)若椭圆上有一点
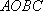
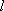
正确答案
(1)
(2)
解析
(1)由已知,可设椭圆方程为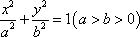
则 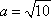
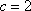
所以 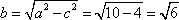
所以 椭圆方程为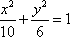
(2)若直线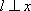
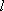
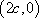
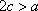
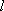

于是,设直线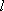
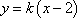
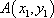
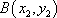
则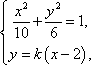

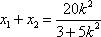
所以 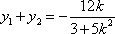
因为 四边形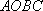
所以 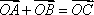
所以 点
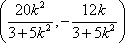
所以 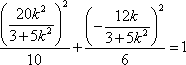
解得
所以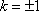
知识点
已知椭圆
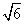
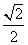
(1)求椭圆的标准方程;
(2)已知点P(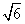
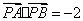
正确答案
见解析
解析
知识点
已知椭圆










(1)求椭圆
(2)过原点





正确答案
见解析
解析
(1)由题意知,




所以椭圆

(2)由题意,当直线


又







当直线


由



设



因为


即,所以


所以点


知识点
扫码查看完整答案与解析