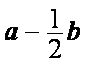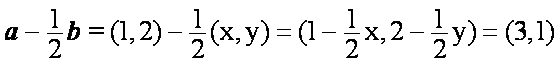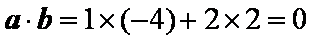- 幂函数的概念、解析式、定义域、值域
- 共1030题
已知f(1,1)=1,f(m,n)∈N*(m、n∈N*),且对任意m、n∈N*都有:
①f(m,n+1)=f(m,n)+2;②f(m+1,1)=2f(m,1)。
给出以下三个结论:(1)f(1,5)=9;(2)f(5,1)=16;(3)f(5,6)=26.其中正确的个数为( )
正确答案
解析
解:∵f(m,n+1)=f(m,n)+2
∴f(1,n)=2n﹣1
故(1)f(1,5)=9正确;
又∵f(m+1,1)=2f(m,1)
∴f(n,1)=2n﹣1
∴(2)f(5,1)=16也正确;
则f(m,n+1)=2m﹣1+2n
∴(3)f(5,6)=26也正确
故选A。
知识点
在平面直角坐标系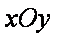
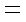
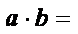
正确答案
0
解析
解析一:设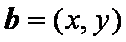
得
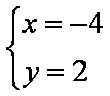
解析二:由a
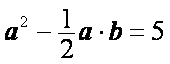
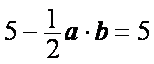
知识点
设



(1)求满足“对任意的




(2)若对任意的






正确答案
见解析。
解析
(1)因为对任意的







(2)当存在一个



当存在二个



其余的由(1)知有

依次类推得:
知识点
已知


(1)若函数

(2)当 

(3)求证
正确答案
见解析。
解析
(1)由题意

所以
当



所以


故

因为函数


所以

即实数

(2)由
令
则
令
因为



所以


所以实数

(Ⅲ)由(Ⅱ) 知
即 
令
所以

……,

所以

所以
所以
知识点
已知函数f(x)=2sinxcosx+2cos2x+1.
(1)求f(x)的最小正周期;
(2)求f(x)在区间
正确答案
(1)
(2)
解析
(1)

所以

(2)因为

所以当


所以

当


所以

知识点
扫码查看完整答案与解析