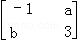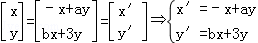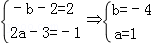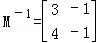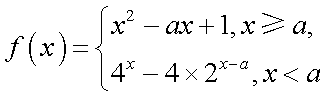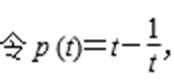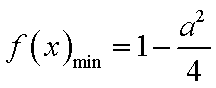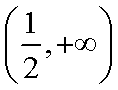- 幂函数的概念、解析式、定义域、值域
- 共1030题
在复平面内,复数
正确答案
解析

知识点
已知a,b∈R,若M=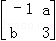
正确答案
见解析。
解析
设P(x,y)为直线2x﹣y=3上任意一点其在M的作用下变为(x',y')
则
代入2x﹣y=3得:﹣(b+2)x+(2a﹣3)y=3其与2x﹣y=3完全一样。
故得
则矩阵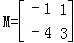
则
知识点
已知函数
(1) 若
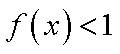
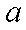
(2) 若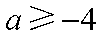
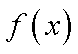
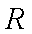
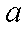
正确答案
见解析
解析
(1) 因为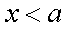
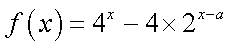
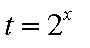
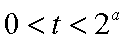
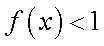
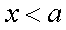
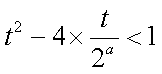
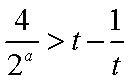
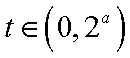
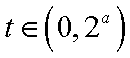
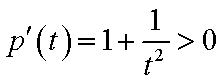
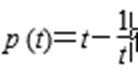
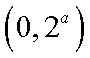
所以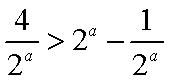

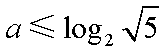
(2) 当
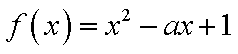
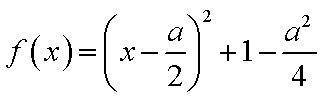
当
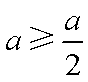
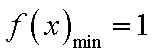
当
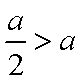
当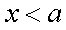
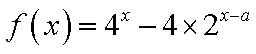
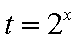
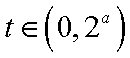
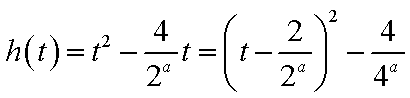
当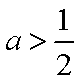
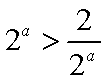
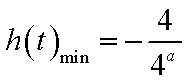
当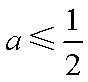
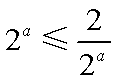
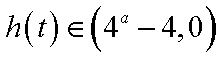
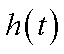
所以,当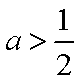
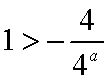
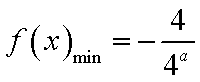
当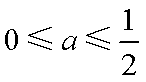
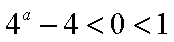
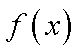
当
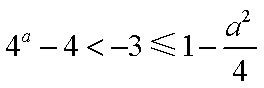
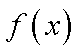
综上所述,当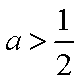
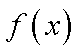
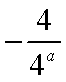
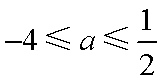
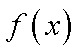
所以函数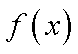
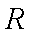
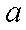
知识点
已知矩阵A的逆矩阵A
正确答案
见解析。
解析
因为A


因为A


于是矩阵A的特征多项式为f (λ)
令f (λ) = 0,解得A的特征值λ1 = -1,λ2 =4
知识点
如图,在四棱锥




(1)求证:

(2)求证:平面

正确答案
见解析
解析
(1)证明:设
而

(2)连接PO,因为


而






又


知识点
在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形

















(1)试分别求出函数

(2)要使得点

正确答案
见解析
解析
解:(1)对于曲线



所以点



则
对于曲线


所以点



(2)因为




为
又



因为

故选用曲线




知识点
如图,⊙




长线上一点,直线

求证:
正确答案
见解析。
解析
连结










∴

∴


知识点
已知函数



正确答案
见解析。
解析


由题设,得

知识点
设函数f(x)=x2+ln(x+1).
(1)求证:当x∈(0,+∞)时f(x)>x恒成立;
(2)求证:
(3)求证:
正确答案
见解析
解析
(1)设g(x)=x-f(x)= x-x2-ln(x+1).
则
当x>0时,g′(x)<0,∴g(x)在(0,+∞)上递减,
∴g(x)<g(0)=0,即x<f(x)恒成立。………5′
(2)由(1)知,x>0时,x-x2<ln(x+1)
令

即
(3)∵y=sinx在[0,1]上单调递增,
∴

又
∴
∴
知识点
已知矩阵


正确答案
见解析。
解析
矩阵M的特征多项式为
令


令


知识点
扫码查看完整答案与解析