- 幂函数的概念、解析式、定义域、值域
- 共1030题
在平面直角坐标系xOy中,直角三角形ABC的三个顶点都在椭圆



正确答案
3
解析
设AB的方程为:






故
所以
令


由




知识点
已知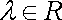
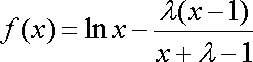
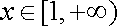
(1)当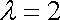
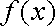
(2)在函数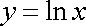
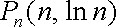
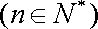
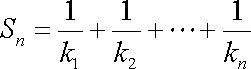
(ⅰ)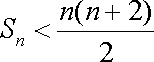
(ⅱ)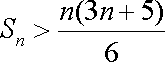
正确答案
见解析
解析
(1)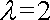
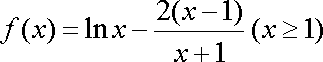
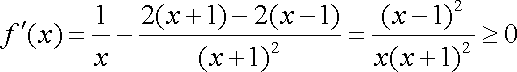
所以,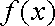
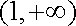
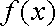
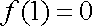
(2)依题意,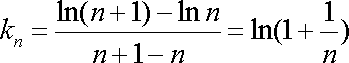
(ⅰ)由(1)可知,若取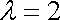
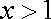
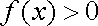
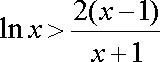
于是 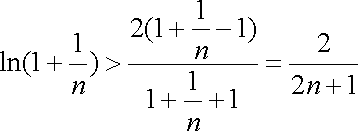
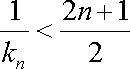
所以 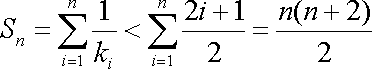
(ⅱ)取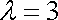
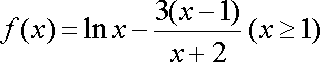
当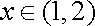
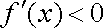
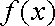
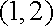
所以,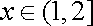
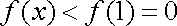
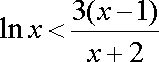
注意到,对任意正整数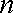
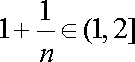
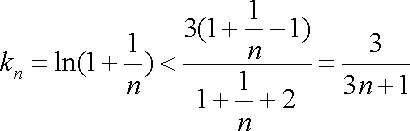
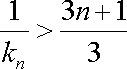
所以 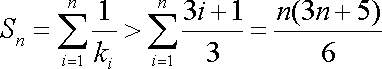
知识点
已知矩阵M
(1) 求矩阵M的逆矩阵;
(2)求矩阵M的特征值及特征向量;
正确答案
见解析
解析
(1)
(2)矩阵A的特征多项式为
令



当




所以特征值

当




所以特征值

知识点
已知

正确答案
解析
由

所以
知识点
已知函数
(1)若



(2) 若


(3)求函数

正确答案
见解析
解析
解:(1)因为


当且仅当x=2时取等号,所以

(2)由题意知,当


所以


则由
(3) 记


①当



②当a<1时,可知2a-1<a,所以
(ⅰ)当




(ⅱ)当




③当

(ⅰ)当




(ⅱ)当





(ⅲ)当



为
综上所述, 函数

知识点
某班级共派出



(1)试求

(2)判断


正确答案
见解析
解析
(1)解:
(2)因为






下用数学归纳法证明
① 当n=1时,该不等式显然成立。
② 假设当




只要证:
令



从而


则当
综合①②, 得原不等式对任意的
知识点
设函数
(1)求
(2)证明:当

(3)证明:当



正确答案
见解析
解析
(1) 



(2)令
由(1)知:






(3)






知识点
设正四棱锥的侧棱长为1,则其体积的最大值为 。
正确答案

解析
法1 设正四棱锥的底面边长为






法2 设正四棱锥的侧棱与底面所成角为






知识点
已知a、b、c均为正实数,且a+b+c=1,求


正确答案
见解析。
解析
因为a、b、c>0,
所以(





≤((a+1)+(b+1)+(c+1))(1+1+1)=12,
于是



当且仅当



所以,



知识点
已知






求证:
正确答案
见解析
解析
设



又

因为


故


知识点
扫码查看完整答案与解析