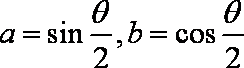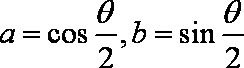- 幂函数的概念、解析式、定义域、值域
- 共1030题
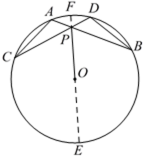
过点P(1,1)的直线将圆x2+y2=4分成两段圆弧,要使这两段弧长之差最大,则该直线的方程为 。
正确答案
x+y﹣2=0
解析
如图所示,当过点P的直线与直径OP垂直时满足直线分成两段圆弧的弧长之差最大,
∵
故所求的直线方程为:y﹣1=﹣(x﹣1),化为x+y﹣2=0。
故答案为x+y﹣2=0。
知识点
已知(x+1)n=a0+a1(x﹣1)+a2(x﹣1)+a3(x﹣1)3+…+an(x﹣1)n,(其中n∈N*)
(1)求a0及
(2)试比较Sn与(n﹣2)2n+2n2的大小,并说明理由。
正确答案
见解析
解析
解:(1)令x=1,则a0=2n,令x=2,
则
(2)要比较Sn与(n﹣2)2n+2n2的大小,即比较:3n与(n﹣1)2n+2n2的大小,
当n=1时,3n>(n﹣1)2n+2n2;当n=2,3时,3n<(n﹣1)2n+2n2;
当n=4,5时,3n>(n﹣1)2n+2n2;
猜想:当n≥4时n≥4时,3n>(n﹣1)2n+2n2,下面用数学归纳法证明:
由上述过程可知,n=4n=4时结论成立,
假设当n=k(k≥4)n=k,(k≥4)时结论成立,即3n>(n﹣1)2n+2n2,
两边同乘以3 得:3k+1>3[(k﹣1)2k+2k2]=k2k+1+2(k+1)2+[(k﹣3)2k+4k2﹣4k﹣2]
而(k﹣3)2k+4k2﹣4k﹣2=(k﹣3)2k+4(k2﹣k﹣2)+6=(k﹣2)2k+4(k﹣2)(k+1)+6>0∴3k+1>[(k+1)﹣1]2k+1+2(k+1)2
即n=k+1时结论也成立,
∴当n≥4时,3n>(n﹣1)2n+2n2成立。
综上得,当n=1时,3n>(n﹣1)2n+2n2;
当n=2,3时,3n<(n﹣1)2n+2n2;当n≥4,n∈N*时,3n>(n﹣1)2n+2n2
知识点
已知
(1)若a=-1,函数f(x)在其定义域内是增函数,求b的取值范围;
(2)当a=1,b=-1时,证明函数f(x)只有一个零点;
(3)f(x)的图象与x轴交于


正确答案
见解析
解析
解析:(1)依题意:
∵f(x)在(0,+∞)上递增,∴
即

∵x>0,∴

∴

(2)当a=1,b=-1时,
∴
∵x>0,∴当0<x<1时,f ′(x)>0;当x>1时,f ′(x)<0。
∴函数f(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,…………6分
∴当x=1时,函数f(x)取得最大值,其值为
当x≠1时,f(x)<f(1),即f(x)<0,∴函数f(x)只有一个零点,…………8分
(3)由已知得
两式相减,得

由
令
∵
∵x1<x2,∴f ′(x0)<0。 …………14分
知识点
如图,⊙

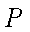
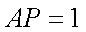
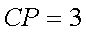
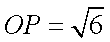
求证:△
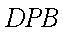
正确答案
见解析。
解析
延长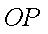
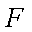
由相交弦定理得
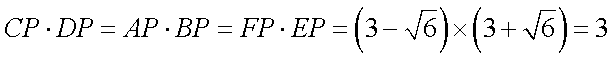
又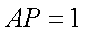
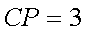
故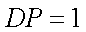
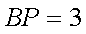
所以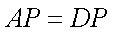
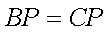
而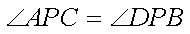
所以△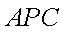
知识点
已知函数


正确答案
解析
∵f(x)=e|x|+x2,∴f(-x)=e|-x|+(-x)2=e|x|+x2=f(x)
则函数f(x)为偶函数且在[0,+∞)上单调递增∴f(-x)=f(x)=f(|-x|)
∴f(3a-2)=f(|3a-2|)>f(a-1)=f(|a-1|),即|3a-2|>|a-1|,两边平方得:8a2-10a+3>0, 解得a<

知识点
设曲线y=(ax﹣1)ex在点A(x0,y1)处的切线为l1,曲线y=(1﹣x)e﹣x在点B(x0,y2)处的切线为l2,若存在
正确答案
解析
解:函数y=(ax﹣1)ex的导数为y′=(ax+a﹣1)ex,
∴l1的斜率为
函数y=(1﹣x)e﹣x的导数为y′=(x﹣2)e﹣x
∴l2的斜率为
由题设有k1•k2=﹣1从而有
∴a(x02﹣x0﹣2)=x0﹣3
∵

又
故

x0=0时取得最大值为

x0=1时取得最小值为1。
∴
知识点
已知函数





(1)求
(2)对任意的正实数

(3)若对任意的


求证:
正确答案
见解析
解析
(1)


所以,





所以,


(2)对任意正实数x1,x2,且x1<x2,取a=x1,则x2∈(x1,+∞)
由(1)得g(x1)>g(x2),即g(x1)=f(x1)—x1f ’(x1)>f(x2)—x2f ’(x1)=g(x2)
所以,f(x2)—f(x1)<(x2—x1)f ’(x1) ……………………①; ……6分
取


即
所以,
综合①②,得
(3)由
所以
=

又由(2)知


所以,
知识点
已知函数
(1)若


(2)当



正确答案
见解析
解析
(1)
(2)
当

当

当

所以解集为
知识点
如图,AB是⊙O的直径,C、E为⊙O上的点,且CA平分∠BAE,DC是⊙O的切线,交AE的延长线于点D,求证:CD⊥AE。
正确答案
见解析。
解析
连接OC,则∠OAC=∠OCA,
又∵CA平分∠BAE,∴∠OAC=∠EAC,
于是∠EAC=∠OCA,∴OC∥AD。
又∵DC是⊙O的切线,
∴CD⊥OC,
∴CD⊥AE。
知识点
给出下列的四个式子:①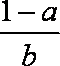
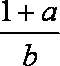
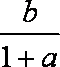
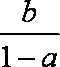
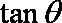
正确答案
解析
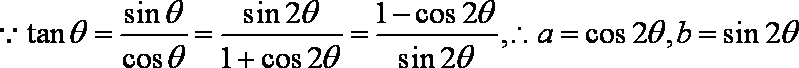
知识点
扫码查看完整答案与解析