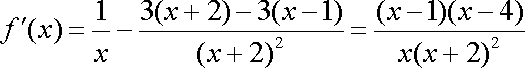- 幂函数的概念、解析式、定义域、值域
- 共1030题
1
题型:填空题
|
在平面直角坐标系xOy中,直角三角形ABC的三个顶点都在椭圆



正确答案
3
解析
设AB的方程为:






故
所以
令


由




知识点
幂函数的概念、解析式、定义域、值域
1
题型:简答题
|
已知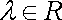
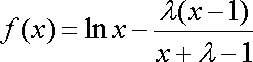
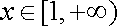
(1)当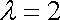
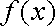
(2)在函数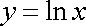
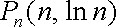
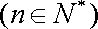
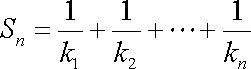
(ⅰ)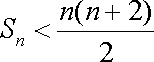
(ⅱ)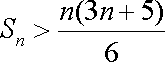
正确答案
见解析
解析
(1)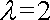
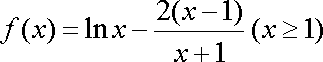
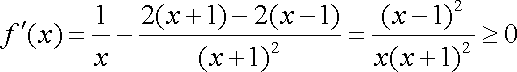
所以,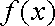
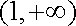
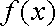
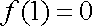
(2)依题意,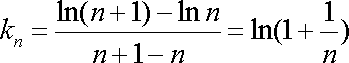
(ⅰ)由(1)可知,若取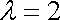
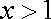
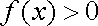
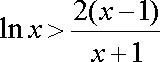
于是 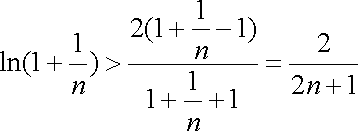
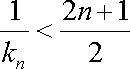
所以 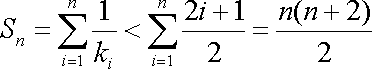
(ⅱ)取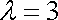
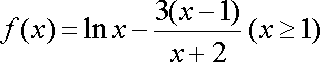
当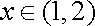
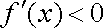
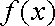
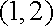
所以,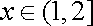
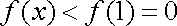
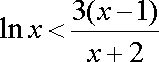
注意到,对任意正整数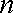
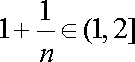
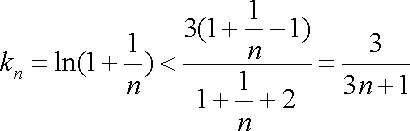
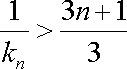
所以 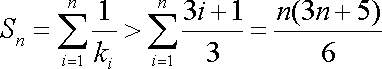
知识点
幂函数的概念、解析式、定义域、值域
1
题型:
单选题
|
已知

正确答案
A
解析
由

所以
知识点
幂函数的概念、解析式、定义域、值域
1
题型:填空题
|
设正四棱锥的侧棱长为1,则其体积的最大值为 。
正确答案

解析
法1 设正四棱锥的底面边长为






法2 设正四棱锥的侧棱与底面所成角为






知识点
幂函数的概念、解析式、定义域、值域
1
题型:简答题
|
已知a、b、c均为正实数,且a+b+c=1,求


正确答案
见解析。
解析
因为a、b、c>0,
所以(





≤((a+1)+(b+1)+(c+1))(1+1+1)=12,
于是



当且仅当



所以,



知识点
幂函数的概念、解析式、定义域、值域
下一知识点 : 幂函数的图像
扫码查看完整答案与解析