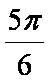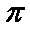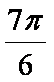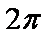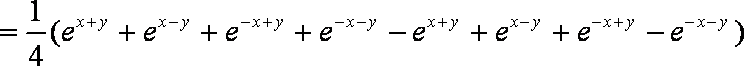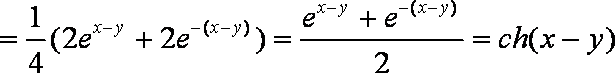- 幂函数的概念、解析式、定义域、值域
- 共1030题
已知函数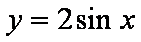
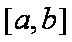
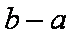
正确答案
解析
值域[-2,1]含最小值不含最大值,故定义域小于一个周期,故选D
知识点
求曲线

正确答案
见解析。
解析
函数



又易判断出在



所以所求面积为
知识点
已知函数

正确答案
解析





知识点
在工程技术中,常用到双曲正弦函数

正确答案
填入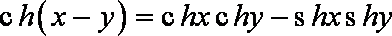
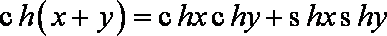
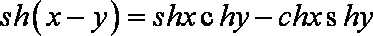
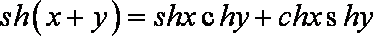
解析
由右边

知识点
在平行四边形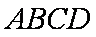
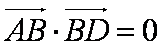
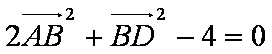
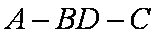
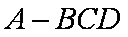
正确答案
解析
折成直二面角后,AC为外接球直径,
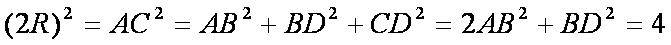
知识点
已知椭圆C:


(1)求椭圆
(2)如图,椭圆左顶点为A,过原点O的直线(与坐标轴不重合)与椭圆C交于P,Q两点,直线PA,QA分别与y轴交于M,N两点,试问以MN为直径的圆是否经过定点(与直线PQ
正确答案
见解析
解析
解析:
(1)由短轴长为

由

∴椭圆

(2)以

证明如下:设



∵



直线


以

【或通过求得圆心

即
∵

令


∴以

知识点
函数
正确答案
解析
函数等价为







知识点
已知





(1)若外接圆O的半径为
(2)求
正确答案
(1)BC=16(2)448
解析
解析:(1)由正弦定理有
∴


且B为钝角,∴

∴
又

(2)由已知

即
同理

两式相减得
即

知识点
变换




(1)求点


(2)求函数


正确答案
见解析。
解析
(1)

所以点


(2)





所以,所求曲线的方程是
知识点
设函数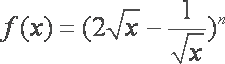
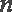
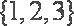
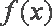
正确答案
解析
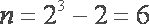
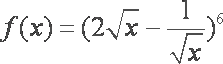
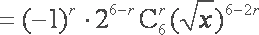

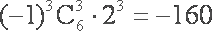
知识点
扫码查看完整答案与解析