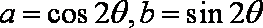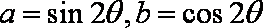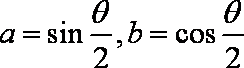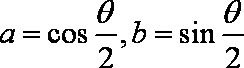- 幂函数的概念、解析式、定义域、值域
- 共1030题
已知
(1)若a=-1,函数f(x)在其定义域内是增函数,求b的取值范围;
(2)当a=1,b=-1时,证明函数f(x)只有一个零点;
(3)f(x)的图象与x轴交于


正确答案
见解析
解析
解析:(1)依题意:
∵f(x)在(0,+∞)上递增,∴
即

∵x>0,∴

∴

(2)当a=1,b=-1时,
∴
∵x>0,∴当0<x<1时,f ′(x)>0;当x>1时,f ′(x)<0。
∴函数f(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,…………6分
∴当x=1时,函数f(x)取得最大值,其值为
当x≠1时,f(x)<f(1),即f(x)<0,∴函数f(x)只有一个零点,…………8分
(3)由已知得
两式相减,得

由
令
∵
∵x1<x2,∴f ′(x0)<0。 …………14分
知识点
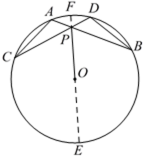
如图,⊙

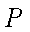
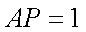
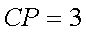
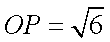
求证:△
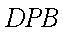
正确答案
见解析。
解析
延长
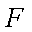
由相交弦定理得
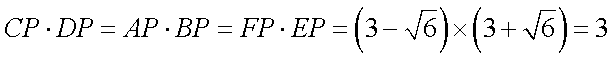
又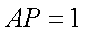
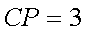
故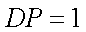
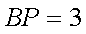
所以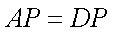
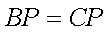
而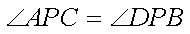
所以△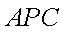
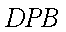
知识点
已知函数
(1)若


(2)当



正确答案
见解析
解析
(1)
(2)
当

当

当

所以解集为
知识点
如图,AB是⊙O的直径,C、E为⊙O上的点,且CA平分∠BAE,DC是⊙O的切线,交AE的延长线于点D,求证:CD⊥AE。
正确答案
见解析。
解析
连接OC,则∠OAC=∠OCA,
又∵CA平分∠BAE,∴∠OAC=∠EAC,
于是∠EAC=∠OCA,∴OC∥AD。
又∵DC是⊙O的切线,
∴CD⊥OC,
∴CD⊥AE。
知识点
给出下列的四个式子:①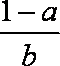
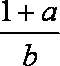
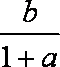
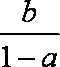
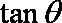
正确答案
解析
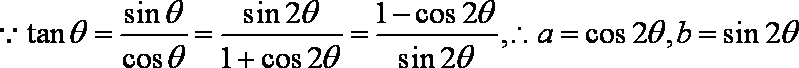
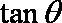
知识点
扫码查看完整答案与解析