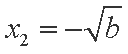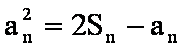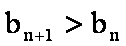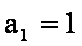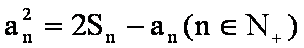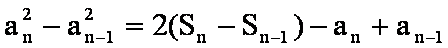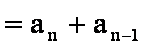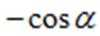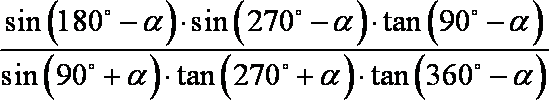- 幂函数的概念、解析式、定义域、值域
- 共1030题
等差数列


正确答案
解析
设等差数列的首项为






知识点
已知函数
(1)当


(2)讨论函数
(3)当


正确答案
(1)


解析
解析:(1)当

∴
∵



∴


而
∴
(2)
①当



②当


③当



∴


综上,
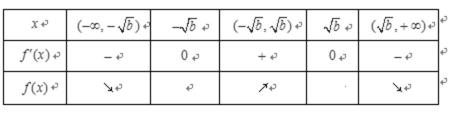
当


当



当


(3)由(2)知,当
即原不等式等价于
即
整理得
∴
又∵


知识点
已知图1是函数y=f(x)的图象,则图2中的图象对应的函数可能是( )
正确答案
解析
由图2知,图象对应的函数是偶函数,故B错误,且当x>0时,对应的函数是y=f(﹣x),显然A、D不正确。故选C
知识点
已知函数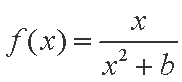
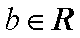
(1)求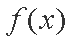
(2)设
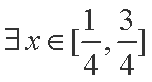
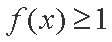
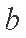
正确答案
见解析
解析
(1)解:① 当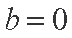
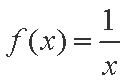
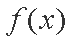
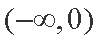
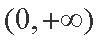
② 当
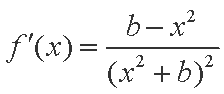
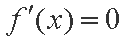
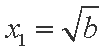
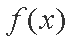
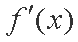
故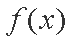
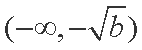
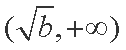
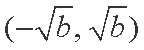
③ 当
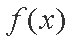
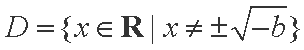
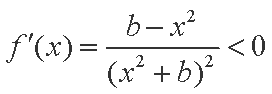
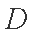
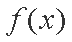
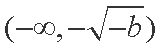
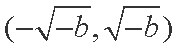
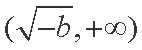
(2)解:因为
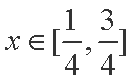
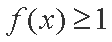
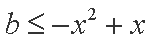
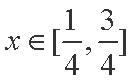
设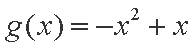
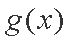
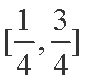
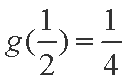
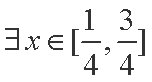
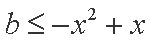
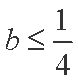
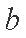
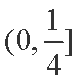
知识点
已知函数
(1)当


(2)是否存在实数



正确答案
(1)2(2)不存在
解析
(1)因为






所以当


所以

(2)不存在. 因为当


所以

而
所以


故不存在实数


(也可构造方程,方程无解,从而得出结论.)
知识点
设f(x)=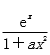
(1)当a=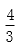
(2)若f(x)为R上的单调函数,求a的取值范围。
正确答案
见解析
解析
解析: 对f(x)求导得f′(x)=ex.①
(1)当a=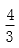
解得x=
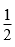
所以,x=
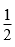
(2)若f(x)为R上的单调函数,则f′(x)在R上不变号,结合①与条件a>0,知ax2-2ax+1≥0在R上恒成立,因此Δ=4a2-4a=4a(a-1)≤0,由此并结合a>0,知0<a≤1.
知识点
设数列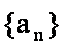
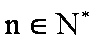

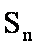
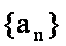
(1)求证:
(2) 求数列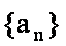
(3)若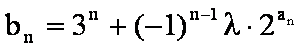
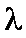
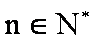
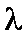
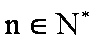
正确答案
见解析
解析
(1)在已知式中,
当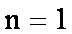
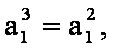
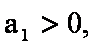

当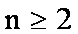
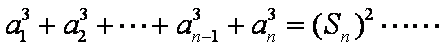
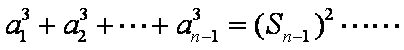
由①-②得,
∵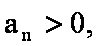
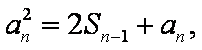
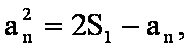


(2)由(1)知, 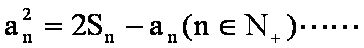
当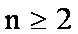
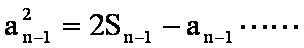
由③-④得,
∵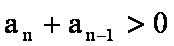
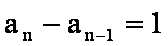
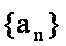
公差为1, 可得
(3) ∵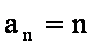
∴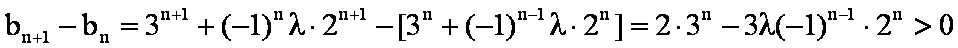
∴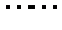
当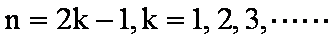
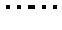
依题意, ⑥式对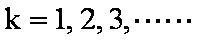
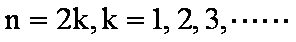
⑤式即为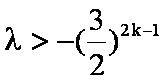
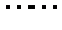
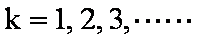
∴
∴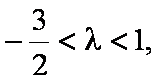
∴存在整数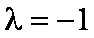


知识点
(1)计算:lg5(lg8+lg1000)+(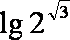
(2)化简
正确答案
(1)1(2)
解析
(1)原式=lg5(3lg2+3)+3lg22-lg6+lg6-2
=3lg5lg2+3lg5+3lg22-2
=3lg2(lg5+lg2)+3lg5-2
=3lg2+3lg5-2
=3(lg2+lg5)-2
=1.
(2)
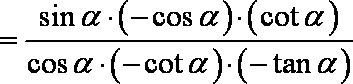

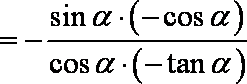
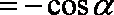
知识点
正确答案
见解析
解析
(1)

显然当







(2)

则



而



若





所以


知识点
设f′(x)是函数f(x)的导函数,有下列命题:
①存在函数f(x),使函数y=f(x)﹣f′(x)为偶函数;
②存在函数f(x)f′(x)≠0,使y=f(x)与y=f′(x)的图象相同;
③存在函数f(x)f′(x)≠0使得y=f(x)与y=f′(x)的图象关于x轴对称。
其中真命题的个数为( )
正确答案
解析
存在函数f(x)=0,使函数y=f(x)﹣f′(x)=0为偶函数,故①正确
存在函数f(x)=ex,使y=f(x)与y=f′(x)的图象相同,故②正确
存在函数f(x)=e﹣x使得y=f(x)与y=f′(x)的图象关于x轴对称,故③正确。
故选D。
知识点
扫码查看完整答案与解析