- 数列与函数的综合
- 共73题
20.已知数列




(Ⅰ)若

(Ⅱ)求证:
(Ⅲ)当


正确答案
解:(I)27,9,3;8,9,3;6,2,3.
(II)若


若



若


所以
所以
所以,对于数列



因为

所以数列

若





由递推关系易得
(III)集合

由已知递推关系可推得数列
当


下面考虑当

按逆序排列各项,构成的数列记为

由(II)的证明过程可知数列




所以,满足



所以



所以



因为


所以


解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数

(1) 求数列
(2) 令
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数



(1)求
(2)若函数




(3)若







正确答案
(1)把
分别代入
可得:
化简此方程组
可得:
即
可得

代入原方程组可得:
(2)由题意知:



即







又


(3)由

即










又
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知:二次函数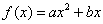
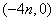
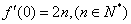
(1)求: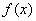
(2)若数列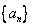
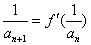
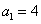
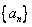
(3)对于(2)中的数列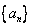
①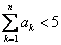
②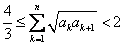
正确答案
解:(1)由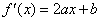
∴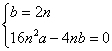
解得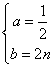
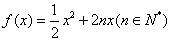
(2)∵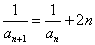
∴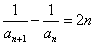
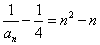
∴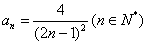
(3)①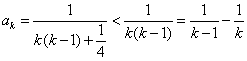
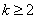
当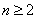
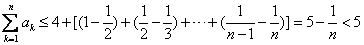
②∵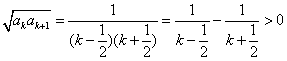
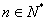
∴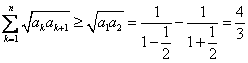
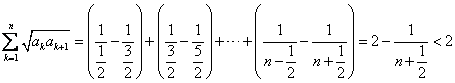
即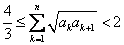
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知函数










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析


















