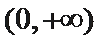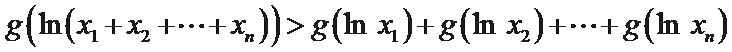- 数列与函数的综合
- 共73题
20.设函数y=f(x)的定义域为(0,+∞),且在(0,+∞)上单调递增,若对任意x,y∈(0,+∞)都有:f(xy)=f(x)+f(y)成立,数列{an}满足:a1=f(1)+1,

(1)求数列{an}的通项公式,并求Sn关于n的表达式;
(2)设函数g(x)对任意x、y都有:g(x+y)=g(x)+g(y)+2xy,若g(1)=1,正项数列{bn}满足:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1) 求
(2) 若



正确答案
(1)


(2)
解析
解析已在路上飞奔,马上就到!
知识点
19.已知


(Ⅰ)判断函数
(Ⅱ) 求证:
(Ⅲ) 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.对于函数f(x)(x∈D),若x∈D时,恒有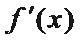
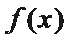
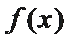
(Ⅰ)当函数f(x)=m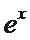
(Ⅱ)若函数g(x)为(0,+∞)上的J函数,试比较g(a)与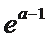
正确答案
解:(Ⅰ)由
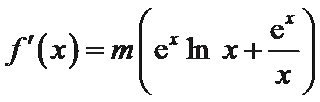
因为函数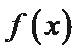
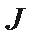
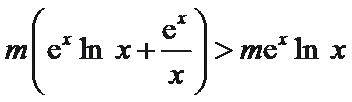
即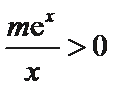
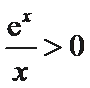
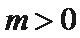
即
(Ⅱ)①构造函数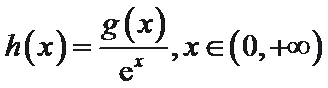
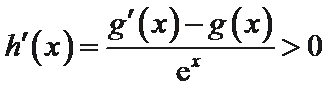
可得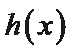
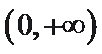
当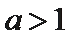
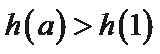
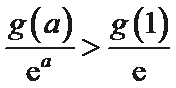
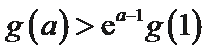
当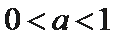
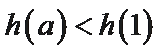
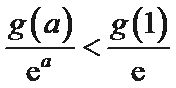
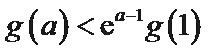
当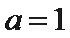
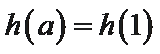
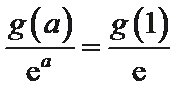
②因为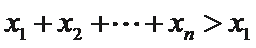
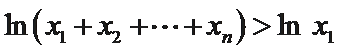
由①可知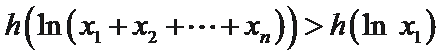

整理得
同理可得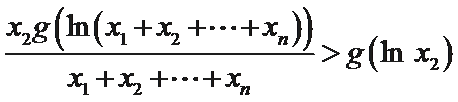
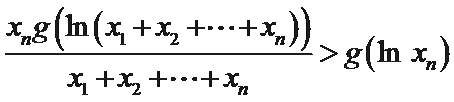
把上面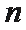
可得
解析
解析已在路上飞奔,马上就到!
知识点
16.已知定义在R上的函数f(x)是奇函数且满足f(





正确答案
-5
解析
知识点
扫码查看完整答案与解析