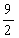- 相似三角形的判定
- 共32题
如图,弦AB与CD相交于O内一点E,过E作BC的平行线与AD的延长线交于点P,已知PD=2DA=2,则PE=__________.
正确答案
解析
∠C与∠A在同一个O中,所对的弧都是

知识点
如图,AD是⊙





.
正确答案


解析
略
知识点
如图所示,等腰三角形ABC的底边AC长0为6,其外接圆的半径长为5,则三角形ABC的面积是 。
正确答案
3
解析
∵等腰三角形ABC的底边AC长为6,其外接圆的半径长为5
∴半径,弦心距和弦长组成一个直角三角形,有勾股定理可知弦心距是 
∴三角形的高是5﹣4=1,
∴三角形的面积是 
故答案为:3。
知识点
如图,M是平行四边形ABCD的边AB的中点,直线l过点M分别交AD,AC于点E,F,若AD=3AE,则AF:FC= 。
正确答案
1:4
解析
如图所示,设直线l交CD的延长线于点N。
∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD。
∵M是边AB的中点,∴
∴

故答案为1:4。
知识点
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过N点的切线交CA的延长线于P。
(1)求证:PM2=PA•PC;
(2)若⊙O的半径为2

正确答案
见解析
解析
(1)证明:连接ON,因为PN切⊙O于N,
∴∠ONP=90°,
∴∠ONB+∠BNP=90°
∵OB=ON,
∴∠OBN=∠ONB
因为OB⊥AC于O,
∴∠OBN+∠BMO=90°,
故∠BNP=∠BMO=∠PMN,PM=PN
∴PM2=PN2=PA•PC
(2)∵OM=2,BO=2
∵BM•MN=CM•MA=(

∴MN=2
知识点
如图,点A、B、C都在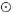
正确答案
解析
略
知识点
选修41:几何证明选讲
如图14,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明:
(1)BE=EC;
(2)AD·DE=2PB2.
正确答案
(1)连接AB,AC.由题设知PA=PD,
故∠PAD=∠PDA.
因为∠PDA=∠DAC+∠DCA,
∠PAD=∠BAD+∠PAB,
∠DCA=∠PAB,
所以∠DAC=∠BAD,从而BE=EC.
因此BE=EC.
(2)由切割线定理得PA2=PB·PC.
因为PA=PD=DC,所以DC=2PB,BD=PB.
由相交弦定理得AD·DE=BD·DC,
所以AD·DE=2PB2.
解析
(1)连接AB,AC.由题设知PA=PD,
故∠PAD=∠PDA.
因为∠PDA=∠DAC+∠DCA,
∠PAD=∠BAD+∠PAB,
∠DCA=∠PAB,
所以∠DAC=∠BAD,从而BE=EC.
因此BE=EC.
(2)由切割线定理得PA2=PB·PC.
因为PA=PD=DC,所以DC=2PB,BD=PB.
由相交弦定理得AD·DE=BD·DC,
所以AD·DE=2PB2.
知识点
如图,已知直线PD切⊙O于点D,直线PO交⊙O于点E,F.若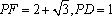
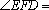
正确答案
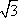
解析
略
知识点
如图所示,C,D是半圆周上的两个三等分点,直径AB=4,CE⊥AB,垂足为E,BD与CE相交于点F,则BF的长为 。
正确答案
解析
∵C,D是半圆周上的两个三等分点,∴∠DBA=30°,
连接AD,则∠ADB=90°,∴AD=2,
过点D作DG⊥AB于G,在Rt△ADG中,∠ADG=30°,∴AG=
则AG=BE=1,∴

故答案为
知识点
如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F,求证BE平分∠ABC。
正确答案
见解析。
解析
∵CD=AC,
∴∠D=∠CAD。
∵AB=AC,
∴∠ABC=∠ACB。
∵∠EBC=∠CAD,
∴∠EBC=∠D。
∵∠ABC=∠ABE+∠EBC,∠ACB=∠D+∠CAD。
∴∠ABE=∠EBC,
即BE平分∠ABC。
知识点
扫码查看完整答案与解析