- 裂项相消法求和
- 共41题
1
题型:填空题
|
15.



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
定积分裂项相消法求和
1
题型:简答题
|
21.设有

(1)求数列{xn}的通项公式;
(2)若
(3)是否存在最小整数m,使得对任意n∈N*,有
正确答案
(1)因方程f(x)=x有唯一解,可求a=

数列{


故

所以数列{xn}的通项公式为
(2)将xn代入an可求得an=2n-1,所以
(3)
即要
解析
解析已在路上飞奔,马上就到!
知识点
由递推关系式求数列的通项公式裂项相消法求和数列与不等式的综合
1
题型:简答题
|
20. 数列



(1)求数列
(2) 记




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
由an与Sn的关系求通项an等比数列的判断与证明裂项相消法求和数列与不等式的综合
1
题型:简答题
|
20. 已知:二次函数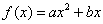
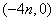
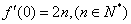
(1)求: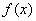
(2)若数列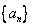
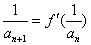
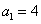
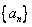
(3)对于(2)中的数列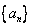
①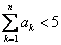
②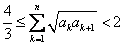
正确答案
解:(1)由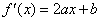
∴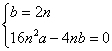
解得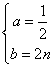
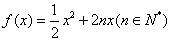
(2)∵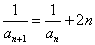
∴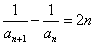
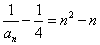
∴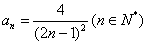
(3)①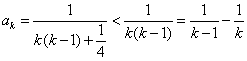
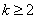
当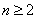
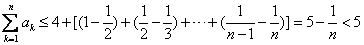
②∵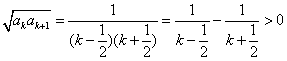
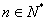
∴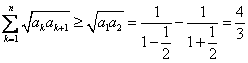
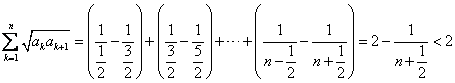
即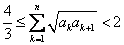
解析
解析已在路上飞奔,马上就到!
知识点
函数解析式的求解及常用方法由递推关系式求数列的通项公式裂项相消法求和数列与函数的综合数列与不等式的综合
1
题型:简答题
|
20.已知数列{an}的前n项和为Sn,Sn=2
(1)求证:数列
(2)设数列{ 2nan}的前n项和为Tn,An=




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
等比数列的判断与证明裂项相消法求和数列与不等式的综合
下一知识点 : 倒序相加法求和
扫码查看完整答案与解析





