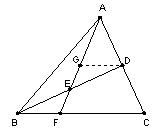- 平面的概念、画法及表示
- 共23题
正确答案
见解析
解析
分别以



则
(1) 证明方法一::







方法二:易证



(2)方法一:设




则















方法二:
设



令
可求得平面

要







(3)可求得平面



知识点
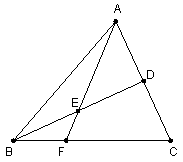
如图,在△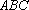
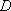
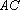
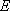
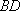
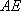
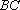
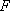
(1)求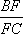
(2)若△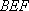
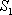
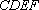
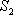
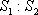
正确答案
见解析。
解析
(1)过D点作DG∥BC,并交AF于G点,∵E是BD的中点,∴BE=DE,
又∵∠EBF=∠EDG,∠BEF=∠DEG,∴△BEF≌△DEG,则BF=DG,
∴BF:FC=DG:FC,又∵D是AC的中点,则DG:FC=1:2,
则BF:FC=1:2;即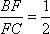
(2)若△BEF以BF为底,△BDC以BC为底,则由(1)知BF:BC=1:3,又由BE:BD=1:2可知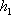
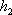
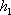
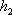
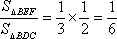
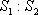
知识点
如图所示,三棱锥









正确答案
见解析
解析
(方法一):取








因为














设


在




在
∴ 异面直线


(方法二):以
















设









设异面直线






∴ 异面直线


知识点
如图6,四棱柱








(1)证明:平面

(2)若

所成角的余弦值。
正确答案
见解析。
解析
(1)依题意,

















(2)取












,所以
(方法二)以













(1)设平面

,








(2)由




所以异面直线

知识点
如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点。
(1)求证:DE∥平面PBC;
(2)求二面角
正确答案
见解析。
解析
(1)
法一 如图,取AB的中点F,连接DF,EF。
在直角梯形ABCD中,CD∥AB,且AB=4,CD=2,所以
所以四边形BCDF为平行四边形,所以DF∥BC,(2分)
在△PAB中,PE=EA,AF=FB,所以EF//PB。
又因为DF

因为DE
法二
取PB的中点M,连接CM,ME。
在△PAB中,PE=EA,PM=MB,所以
在直角梯形ABCD中,CD∥AB,且AB=4,CD=2,
故

所以四边形CDEM为平行四边形,故DE∥CM。
因为CM

所以DE∥平面PBC,(4分)
(2)取AD的中点O,BC的中点N,连接ON,则ON∥AB。
在△PAD中,PA=PD=AD=2,所以PO⊥AD,
又因为平面PAD⊥平面ABCD,平面PAD
所以PO⊥平面ABCD,(6分)
如图,以O为坐标原点;分别以OA,ON,OP所在直线为





因为E为PA的中点,所以


因为平面PAD⊥平面ABCD,平面PAD
所以PO⊥平面ABD,故
设平面EBD的法向量为
由


令



所以
设二面角



知识点
扫码查看完整答案与解析