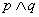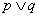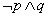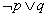- 绝对值不等式的解法
- 共46题
不等式
正确答案
[-3,1]
解析
略
知识点
设命题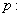
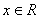
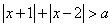
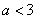
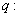
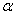
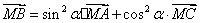
正确答案
解析
略
知识点
已知

(1)当


(2)求函数

正确答案
见解析
解析
(1)由题意,
当


当


综上,所求解集为
(2)①当



∵
∴
∴
② 当


③当









∴综上,
知识点
已知函数



正确答案

解析
略
知识点
设
(1)当

(2)若对任意x∈R,

正确答案
见解析
解析
解析:
(1)f(x)=|x-a|≤3,即a-3≤x≤a+3.依题意,
由此得a的取值范围是[0,2],
(2)f(x-a)+f(x+a)=|x-2a|+|x|≥|(x-2a)-x|=2|a|,
当且仅当(x-2a)x≤0时取等号, 解不等式2|a|≥1-2a,得a≥。
故a的最小值为。
知识点
设函数
(1)求不等式
(2)若关于x的不等式


正确答案
见解析
解析
解析:(1)

(2)只要
由(1)知

知识点
已知关于x的不等式|ax﹣1|+|ax﹣a|≥1的解集为R,求正实数a的取值范围。
正确答案
见解析。
解析
因为|ax﹣1|+|ax﹣a|≥|a﹣1|,故原不等式解集为R等价于|a﹣1|≥1.所以a≥2,或a≤0。
又因为a>0,所以a≥2,所以正实数a的取值范围为[2,+∞)。
知识点
已知函数
(1)解不等式
(2)若

正确答案
见解析
解析
(1)f(x)+f(x+4)=|x-1|+|x+3|=
当x<-3时,由-2x-2≥8,解得x≤-5;
当-3≤x≤1时,f(x)≤8不成立;
当x>1时,由2x+2≥8,解得x≥3. …4分
所以不等式f(x)≤4的解集为{x|x≤-5,或x≥3}, …5分
(2)f(ab)>|a|f(),即|ab-1|>|a-b|, …6分
因为|a|<1,|b|<1,所以|ab-1|2-|a-b|2
=(a2b2-2ab+1)-(a2-2ab+b2)
=(a2-1)(b2-1)>0,
所以|ab-1|>|a-b|,故所证不等式成立, 10分
知识点
设函数
(1)解不等式
(2)求函数
正确答案
见解析。
解析
(1)
不等式


解得:



(2)根据函数的单调性可知函数

此时
知识点
已知关于

(1)求整数
(2)已知


正确答案
(1)m=4(2)
解析
(1)

又不等式仅有一个整数解2, 
(2)显然
由柯西不等式可知;
所以
当且仅当

知识点
扫码查看完整答案与解析