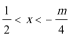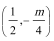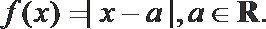- 绝对值不等式的解法
- 共46题
8.不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数
(1)作出函数



(2)关于


(3)关于



正确答案
(1)解:
(作图如下:)
已知当

(2)

即方程
当
(3)关于


即
数形结合可知必有


令



解析
解析已在路上飞奔,马上就到!
知识点
13.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知集合



正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数
(1)若

(2)当方程

(3)若对于一切


正确答案
(1)由
当

当




所以不等式
(2)由
令
由函数图像知两函数图像在y轴右边只有一个交点时满足题意

由
(3)
当


所以
当
①当


令


所以


所以
所以
②当

即
所以
综上,
解析
解析已在路上飞奔,马上就到!
知识点
14. 设有两个命题:
(1)不等式|x|+|x-1|>m的解集为R;
(2)定义在R上的函数
这两个命题中有且只有一个命题是真命题,则m的取值范围是___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第(22)、(23)两题中任选一题作答。注意:只能做所选定的题目。如果多做,则按所做的第一个题目计分。
22.如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T,(不与a、b重合),DN与圆O相切于点N,连结MC,MB,OT。
(I)求证:
(II) 若

23.已知函数
(I)解不等式 
(II)若


正确答案
22.(1)证明:因MD与圆O相交于点T,由切割线定
理




则

所以
(2)由(1)可知,

故


根据圆周角定理得,
23.(1)由题
因此只须解不等式
当


当


当


综上,原不等式的解集为
(2)由题
当

解析
解析已在路上飞奔,马上就到!
知识点
18.设函数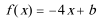
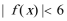
(1)求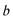
(2)解不等式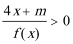
正确答案
(1)∵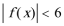
∴
(2)由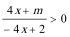
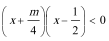
①当
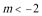
②当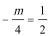
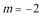
③当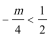
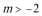
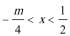
∴当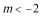
当
当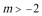

解析
解析已在路上飞奔,马上就到!
知识点
18.设
(1)当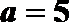
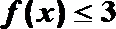
(2)当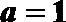
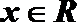
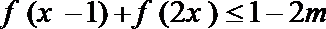

正确答案
(1)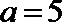
即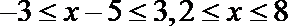
所以解集为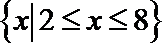
(2)当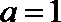
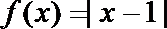
令
由图像知:
当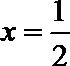
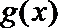

由题意知: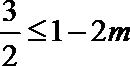
所以实数

解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析