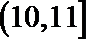- 函数的最值及其几何意义
- 共151题
20.已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大。(注:年利润一年销售收入一年总成本)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(Ⅰ)当
(Ⅱ) 当




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知复数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.
(1) 设半圆的半径OA=r (米),试建立塑胶跑道面积S与r的函数关系S(r);
(2) 由于条件限制r∈[30,40],问当r取何值时,运动场造价最低?(精确到元)
正确答案
(1) 塑胶跑道面积
(2) 设运动场造价为y,
则 
∵r∈[30,40],函数y是r的减函数,
∴当r=40时,运动场造价最低为636510元
解析
解析已在路上飞奔,马上就到!
知识点
9.在等比数列{an}中,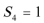
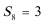
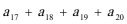
正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
12.设等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.命题






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.不等式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
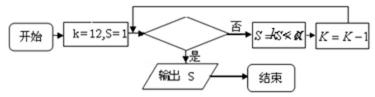
9.程序框图如下:如果上述程序运行的结果为S=132,那么判断框中实数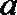
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 在直角坐标系中, 如果两点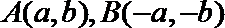
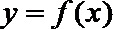
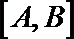
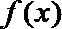
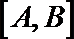
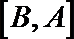
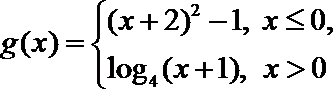
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析