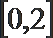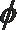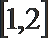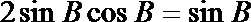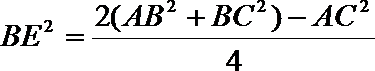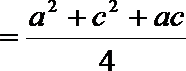- 函数的最值及其几何意义
- 共151题
1.已知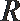
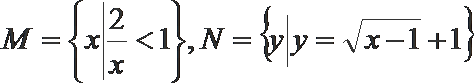
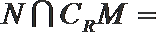
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在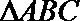
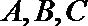
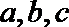

(1)求角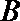
(2)若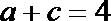
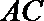
正确答案
(1)由题意得: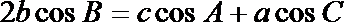
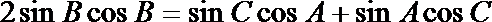

(2)设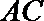
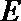
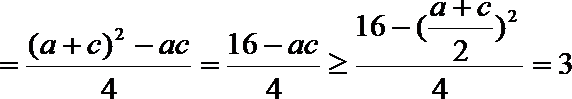
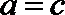
所以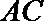
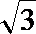
解析
解析已在路上飞奔,马上就到!
知识点
21.已知


(1)求
(2)是否存在实数a,使得当
正确答案
(1)设

故函数
(2)假设存在实数a,使得当

①当
由于



②当

综上所知,存在实数

解析
解析已在路上飞奔,马上就到!
知识点
19.已知关于


(1)当

(2)对于不等式的解集





正确答案
当


当

(2) 由(1)知:当

当


因为

所以当

此时

解析
解析已在路上飞奔,马上就到!
知识点
8.在





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在平面直角坐标系





正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
12.对于函数









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知命题










正确答案
解:p真,任意

即

则a≤1
q真,则△=(a-1)2-4>0,即a>3或a<-1
∵“p或q”为真,“p且q”为假,∴p,q中必有一个为真,另一个为假
当p真q假时,有
当p假q真时,得a>3
∴实数a的取值范围为-1≤a≤1或a>3
解析
解析已在路上飞奔,马上就到!
知识点
9.设函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 在复平面内与复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析