函数的最值及其几何意义
共151题

· 函数的最值及其几何意义

函数的最值及其几何意义
共151题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

已知.

（1）记在区间上的最大值为，求的表达式；

（2）是否存在a，使函数在区间（0，9）内的图象上存在两点，在该两点处的切线互相垂直？若存在，求a的取值范围；若不存在，请说明理由.

正确答案

见解析

解析

知识点

函数解析式的求解及常用方法函数的最值及其几何意义导数的几何意义

题型：单选题

单选题 · 5 分

某购物网站在2013年11月开展“全场6折”促销活动，在11日当天购物还可以再享受“每张订单金额（6折后）满300元时可减免100元”.某人在11日当天欲购入原价48元（单价）的商品共42件，为使花钱总数最少，他最少需要下的订单张数为（）

正确答案

解析

略

知识点

函数的最值及其几何意义

题型：简答题

简答题 · 14 分

已知函数（为常数）。

（1）函数的图象在点（）处的切线与函数的图象相切，求实数的值；

（2）若，、使得成立，求满足上述条件的最大整数；

（3）当时，若对于区间[1,2]内的任意两个不相等的实数，，都有

成立，求的取值范围。

正确答案

见解析。

解析

（1）∵，∴，，

∴函数的图象在点（）处的切线方程为，

∵直线与函数的图象相切，由消去y得，

则，解得-

（2）当时，∵，

∴，-

当时，，∴在上单调递减，

，-

则，

∴,故满足条件的最大整数.-

（3）不妨设，∵函数在区间[1,2]上是增函数，∴，

∵函数图象的对称轴为，且，∴函数在区间[1,2]上是减函数，

∴，-

∴等价于，

即，

等价于在区间[1,2]上是增函数，

等价于在区间[1,2]上恒成立，

∴，又，∴.-

知识点

函数单调性的性质函数的最值及其几何意义导数的几何意义

题型：单选题

单选题 · 5 分

已知命题：：函数在R上为增函数；：函数在R上为减函数。

则在命题：，：，：和：中，真命题是（）

A，

B，

C，

D，

正确答案

解析

为真命题，对于，，显然导函数可正可负，

因此是假命题，因此、为真命题，、为假命题。

知识点

函数的最值及其几何意义

题型：填空题

填空题 · 5 分

已知，函数，若函数在区间[0,2]上的最大值比

最小值大，则a的值为________.

正确答案

解析

略

知识点

函数的最值及其几何意义

题型：简答题

简答题 · 14 分

某通讯公司需要在三角形地带区域内建造甲、乙两种通信信号加强中转站，甲中转站建在区域内，乙中转站建在区域内，分界线固定，且=百米，边界线始终过点，边界线满足。

设（）百米，百米.

（1）试将表示成的函数，并求出函数的解析式；

（2）当取何值时？整个中转站的占地面积最小，并求出其面积的最小值。

正确答案

（1）（2）当米时，整个中转站的占地面积最小，最小面积是平方米

解析

（1）结合图形可知，，

于是，，

解得，

（2）由（1）知，，

因此，

（当且仅当，即时，等号成立），

答：当米时，整个中转站的占地面积最小，最小面积是平方米

知识点

函数解析式的求解及常用方法函数的最值及其几何意义利用基本不等式求最值

题型：填空题

填空题 · 5 分

关于函数，有下列命题：

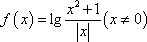
①其图象关于y轴对称；

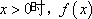
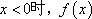
②当是增函数；当是减函数；

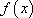
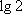
③的最小值是；

④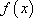在区间上是增函数；

⑤无最大值，也无最小值.

其中所有正确结论的序号是_____________.

正确答案

解析

略

知识点

命题的真假判断与应用函数单调性的判断与证明函数的最值及其几何意义

题型：填空题

填空题 · 5 分

记实数中的最大数为，最小数为.设△的三边边长分别为，且，定义△的倾斜度为。

（ⅰ）若△为等腰三角形，则______；

（ⅱ）设，则的取值范围是______。

正确答案

，

解析

略

知识点

函数的最值及其几何意义不等式的性质

题型：单选题

单选题 · 5 分

某企业为节能减排，用9万元购进一台新设备用于生产. 第一年需运营费用2万元，从第二年起，每年运营费用均比上一年增加2万元，该设备每年生产的收入均为11万元. 设该设备使用了年后，年平均盈利额达到最大值（盈利额等于收入减去成本），则n等于（）

正确答案

解析

略

知识点

函数的最值及其几何意义

题型：简答题

简答题 · 14 分

设函数，；，.

（1）求函数的单调区间；

（2）当时，求函数的最大值；

（3）设，且，，证明：.

正确答案

见解析。

解析

（1）显然的定义域为，，

令，

ⅰ）当时：在区间上，恒成立，故的增区间为；

ⅱ）当时：在区间上，恒成立，故的减区间为；

在区间上，恒成立，故的增区间为.

（2）ⅰ）时，，所以；

ⅱ）时，易知，

于是：，，

由（1）可知，下证，

即证明不等式在上恒成立。

（法一）由上可知：不等式在上恒成立，

若，则，

故，

即当时，，从而，

故当时，恒成立，即.

（法二）令，，则，列表如下：

由表可知：当时，，

即恒成立，即.

由于，且，

故函数区间内必存在零点。

又当时，，

于是指数函数为增函数为增函数，

同理当时，，

于是指数函数为减函数也为增函数，

于是，当时，必为增函数，

从而函数在区间内必存在唯一零点，不妨记为，则，

易知当时，，此时单调递减；

当时，，此时单调递增，

又易知，故；

综上，当时，在上的最大值为.

（3）证法一：令，显然有：，，

则不等式.

注意到：，且，，即，且，

于是，，

故，

从而，即，又，

故原不等式成立，证毕.

证法二：同上可将不等式化为：,

即，令，则等价于证明：当时，有成立，

又，

故，

于是，即得证，

又，故原不等式成立，证毕。

知识点

函数单调性的性质函数的最值及其几何意义数列与函数的综合数列与不等式的综合

继续学习学习下一知识点

下一知识点 : 奇函数

百度题库 > 高考 > 理科数学 > 函数的最值及其几何意义

扫码查看完整答案与解析