函数的最值及其几何意义
共151题

· 函数的最值及其几何意义

函数的最值及其几何意义
共151题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

在实数集中定义一种运算“”，对任意，为唯一确定的实数，且具有性质：

（1）对任意，；

（2）对任意，。

关于函数的性质，有如下说法：①函数的最小值为；②函数为偶函数；③函数的单调递增区间为。

其中所有正确说法的个数为

正确答案

解析

略

知识点

命题的真假判断与应用函数单调性的判断与证明函数的最值及其几何意义函数奇偶性的判断

题型：单选题

单选题 · 5 分

函数的图象大致是

正确答案

解析

略

知识点

函数的最值及其几何意义

题型：填空题

填空题 · 5 分

函数的最大值是。

正确答案

解析

略

知识点

函数的最值及其几何意义

题型：简答题

简答题 · 13 分

设是由个有序实数构成的一个数组，记作：.其中称为数组的“元”，称为的下标. 如果数组中的每个“元”都是来自数组中不同下标的“元”，则称为的子数组. 定义两个数组，的关系数为.

（1）若，，设是的含有两个“元”的子数组，求的最大值；

（2）若，，且，为的含有三个“元”的子数组，求的最大值；

（3）若数组中的“元”满足.设数组含有四个“元”，且，求与的所有含有三个“元”的子数组的关系数的最大值。

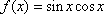
正确答案

见解析

解析

（1）依据题意，当时，取得最大值为2.

（2）①当是中的“元”时，由于的三个“元”都相等及中三个“元”的对称性，可以只计算的最大值，其中。

由，

得，当且仅当，且时，达到最大值，

于是，

②当不是中的“元”时，计算的最大值，由于，

所以。，

当且仅当时，等号成立，即当时，取得最大值，

此时，综上所述，的最大值为1.

（3）因为满足。

由关系的对称性，只需考虑与的关系数的情况。

当时，有。

。

即，且，，时，的最大值为。

当时，，得最大值小于。

所以的最大值为。

知识点

函数的最值及其几何意义

题型：填空题

填空题 · 5 分

函数是定义在上的偶函数，且满足.当时，.若在区间上方程恰有四个不相等的实数根，则实数的取值范围是（）.

正确答案

解析

略

知识点

函数的最值及其几何意义

题型：简答题

简答题 · 13 分

已知函数。

（1）当时，求函数在上的最大值和最小值；

（2）若，讨论的单调性。

正确答案

见解析

解析

（1）解：的定义域为，………………………，1分

当时， ………………………，2分

令在上得极值点

………………………，4分

………………………，5分

， …………………，7分

（2）解：， ………………………，8分

①时，由得或，所以的单调增区间是，

由得，所以的单调减区间是； ………………………，10分

②时，在上恒成立，且当且仅当，

在单调递增； ………………………，11分

③当时，由得或，所以的单调增区间是，

由得，所以的单调减区间是， ………………………，13分

知识点

函数的最值及其几何意义

题型：简答题

简答题 · 12 分

一个袋中装有形状大小完全相同的球9个，其中红球3个，白球6个，每次随机取1个，直到取出3次红球即停止。

（1）从袋中不放回地取球，求恰好取4次停止的概率P1；

（2）从袋中有放回地取球。

①求恰好取5次停止的概率P2；

②记5次之内(含5次)取到红球的个数为，求随机变量的分布列及数学期望。

正确答案

见解析

解析

知识点

函数的最值及其几何意义

题型：填空题

填空题 · 5 分

已知，函数若函数在上的最大值比最小值大，则的值为 .

正确答案

解析

略

知识点

函数的最值及其几何意义

题型：简答题

简答题 · 12 分

已知函数（其中，，）的最大值为2，最小正周

期为.

（1）求函数的解析式；

（2）若函数图象上的两点的横坐标依次为，为坐标原点，求△ 的

面积。

正确答案

见解析。

解析

（1）解：∵的最大值为2，且， ∴.

∵的最小正周期为， ∴，得.

∴.

（2）解法1：∵，

，

∴.

∴△的面积为

解法2：∵，

，

∴.

∴△的面积为.

解法3：∵，

，

∴.

∴直线的方程为，即.

∴点到直线的距离为.

∵，

∴△的面积为.

知识点

函数的最值及其几何意义

题型：填空题

填空题 · 5 分

某同学为研究函数的性质，构造了如图所示的两个边长为1的正方形和，点是边上的一个动点，设，则. 请你参考这些信息，推知函数的图象的对称轴是（）；函数的零点的个数是（） .

正确答案

；2

解析

略

知识点

函数的最值及其几何意义函数零点的判断和求解

继续学习学习下一知识点

下一知识点 : 奇函数

百度题库 > 高考 > 理科数学 > 函数的最值及其几何意义

扫码查看完整答案与解析