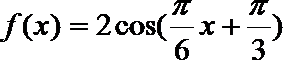- 函数的最值及其几何意义
- 共151题
16．已知函数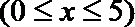
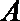
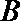
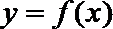
（1）求点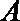
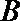
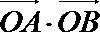
（2）设点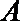
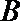
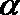
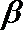
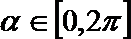
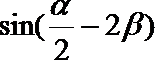
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．(ax＋1)8的展开式中x5的系数是56，则a＝___________。
正确答案
1
解析
解析已在路上飞奔，马上就到！
知识点
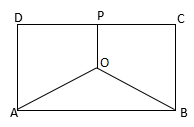
17.某地有三家工厂，分别位于矩形ABCD的顶点A、B及CD的中点P处，已知AB=20km，BC=10km，为了处理三家工厂的污水，现要在矩形ABCD的区域上（含边界），且A、B与等距离的一点O处建造一个污水处理厂，并铺设排污管道AO、BO、OP，设排污管道的总长为ykm。
（1）按下列要求写出函数关系式：
①设∠BAO=θ（rad），将y表示成θ的函数关系式；
②设OP=x（km），将y表示成x的函数关系式；
（2）请你选用（1）中的一个函数关系式，确定污水处理厂的位置，使三条排污管道总长度最短。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1． 已知数集
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．某出版社新出版一本高考复习用书，该书的成本为5元一本，经销过程中每本书需付给代理商
（1）求该出版社一年的利润L（万元）与每本书的定价
（2）若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20.已知
（1）求
（2）是否存在负实数
（3）对
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11.记min{a,b}为a、b两数的最小值,当正数x、y变化时,t= 
A
B
C
D
正确答案
解析
(1)若
则t=x,
故t≤
当且仅当x=y= 
(2)若
则
故
当且仅当x=y= 
综上可知,
当x=y= 
知识点
9.已知在正四棱锥S-ABCD中,SA=
A1
B
C2
D3
正确答案
解析
设底面边长为a,
则高
,所以体积
设
则y'=12a3-3a5,当y取最值时,y'=0,
解得a=0(舍去)或a=2,
所以当该棱锥的体积最大时,h=1,
故选A.
知识点
11.记min{a,b}为a、b两数的最小值,当正数x、y变化时,t= 
A
B
C
D
正确答案
解析
(1)若
则t=x,
故t≤ ,
当且仅当x=y= 
(2)若
则
故
当且仅当x=y= 
综上可知,
当x=y= 
知识点
15. 如图,球
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析