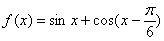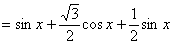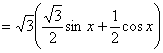- 函数的最值及其几何意义
- 共151题
已知

(1)设







(2)如图,若











正确答案
见解析
解析
(1)由题意,可设
将

得


(2)以




设







于是
故当


另解:设





于是
故当


知识点
已知函数










正确答案
-3
解析
由题意知:

可解得:
因为

因为


当且仅当


所以,当


知识点
定义

(1)设


(2)设


(3)记(2)中最小值为


正确答案
见解析。
解析
知识点
直线




正确答案
解析
略
知识点
设函数


(1)求

(2)是否存在两个不等正数




正确答案
见解析。
解析
(1)
依题意则有:

∴
令

当


所以函数

(2)由函数的定义域是正数知,


①若极值点





②若



则


③若


两式相减并除

两式相除可得



由①、②可得


即存在

综上可得不存在满足条件的s、t.
知识点
已知函数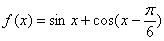
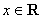
(1)求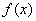
(2)设△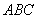
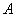
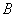
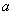
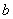
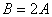
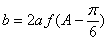
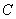
正确答案
见解析。
解析
(1)
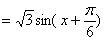
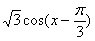
所以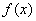
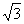
(2)因为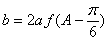
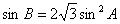
又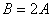
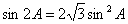
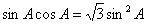
而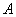
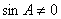
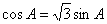
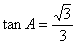
所以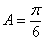
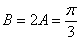
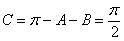
知识点
已知函数



(1)求实数
(2)求

(3)对任意给定的正实数


正确答案
见解析。
解析
(1)当

由题意,得


(2)由(1),知
①当










因为




②当






所以


所以当



当


(3)假设曲线

因为△POQ是以O为直角顶点的直角三角形,所以
不妨设




是否存在两点P,Q满足题意等价于方程(*)是否有解。
若


即
当



设


所以




因为


所以当

所以对任意给定的正实数


知识点
已知四棱柱




正确答案
解析
由条件可得,A、M、P、N四点在以PA为直径的圆上,所以由正弦定理得






知识点
函数
正确答案
解析
略
知识点
某工厂生产某种产品,已知该产品的月生产量

正确答案
见解析。
解析
每月生产x吨时的利润为
由
得当 
∴
故
答:每月生产200吨产品时利润达到最大,最大利润为315万元.
知识点
扫码查看完整答案与解析