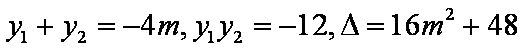- 函数的最值及其几何意义
- 共151题
在平面直角坐标系




正确答案
见解析。
解析
直线l的普通方程为:

∴当


知识点
已知函数f(x)=ax+lnx,其中a为常数,设e为自然对数的底数。
(1) 当a=-1时,求f(x)的最大值;
(2) 若f(x)在区间(0,e]上的最大值为-3,求a的值;高考资源网
(3) 当a=-1时,试推断方程

正确答案
见解析。
解析
(1)当a=-1时,f(x)=-x+lnx,f′(x)=-1+
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数…………3分

(2)∵f′(x)=a+


① 若a≥
∴
② 若a<

由f(x)<0

从而f(x)在

∴


令-1+ln

∴





(3) 由(1)知当a=-1时
∴|f(x)|≥1……………………………………………………………10分
又令g(x)=

当0<x<e时,g′(x)>0,g(x) 在(0,e)单调递增高考资源网;
当x>e时,g′(x)<0,g(x) 在(e,+∞)单调递减…………………………11分
∴

∴|f(x)|>g(x),即|f(x)|> 
∴方程|f(x)|=
知识点
某种商品每件进价12元,售价20元,每天可卖出48件,若售价降低,销售量可以增加,且售价降低

(1)试将该商品一天的销售利润表示成
(2)该商品售价为多少元时一天的销售利润最大?
正确答案
见解析
解析
(1)由题意可设,每天多卖出的件数为

又每件商品的利润为
∴该商品一天的销售利润为
(2)由
令

当


∴当商品售价为16元时,一天销售利润最大,最大值为432元
知识点
已知函数

(1)当

(2)是否存在等差数列


正确答案
见解析。
解析
(1)



令

因为

当

所以当



当

所以



(2)假设存在等差数列

由组合数的性质
把等式变为
两式相加,因为

故
所以
再分别令


进一步可得满足题设的等差数列

知识点
动点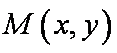
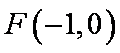
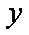
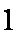
(1)求动点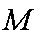
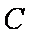
(2)过点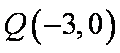
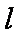
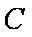
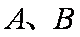
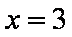
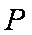
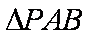
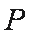
正确答案
见解析
解析
解析:(1)依题意有: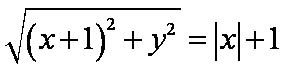
当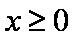
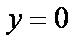
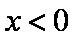
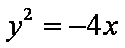
∴M点的轨迹方程为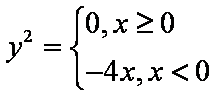
(2)分析可知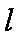
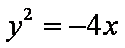
设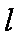
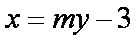
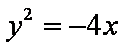
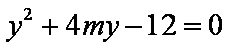
设A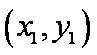
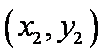
∴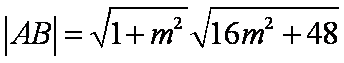
AB的中点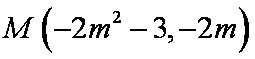
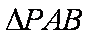
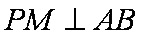
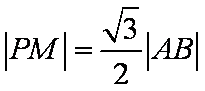
令点P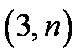

∴
所以存在点P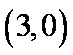
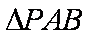
知识点
扫码查看完整答案与解析