- 函数的最值及其几何意义
- 共151题
某地区的农产品A第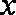
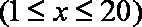
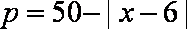
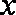
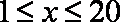
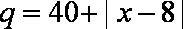
(1)求该农户在第7天销售家产品A的收入;
(2)问这20天中该农户在哪一天的销售收入最大?
正确答案
(1)2009(元)(2)第2天该农户的销售收入最大
解析
(1)由已知第7天的销售价格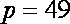
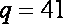
所以第7天的销售收入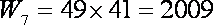
(2)设第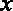
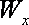
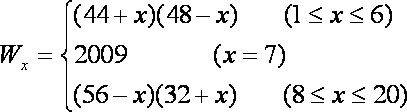
当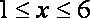
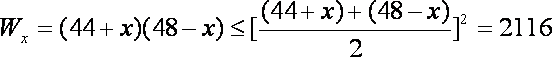
当且仅当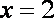
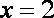
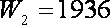
当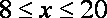
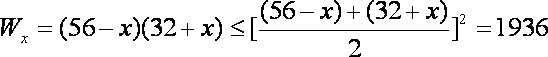
当且仅当

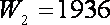

由于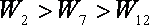
所以第2天该农户的销售收入最大.……………………………………………………12分
知识点
已知函数
(1)若曲线





(2)在(1)的条件下,试求函数


(3)若


正确答案
见解析
解析
解析:(1)












由①②得:
(2)由(1)知:




当





由表可知:

当




由表可知:

综上可知:当


当

(3)因为


即

∴
由 (1)+(3)得:
由(4)得:



故
知识点
已知
(1)求f(x)的最大值及取到最大值时相应的x的集合;-
(2)若函数
正确答案
见解析
解析
(1)
最大值为


(1)
知识点
已知函数f(x)=(sin2x+cos2x)2﹣2sin22x。
(1)求f(x)的最小正周期;
(2)若函数y=g(x)的图象是由y=f(x)的图象向右平移

正确答案
见解析。
解析
(1)因为f(x)=(sin2x+cos2x)2﹣2sin22x=sin4x+cos4x=
所以函数f(x)的最小正周期为
(2)依题意,y=g(x)=


因为

当


当
知识点
设等轴双曲线





正确答案
6
解析
等轴双曲线的渐近线为








知识点
已知函数
(1)若
(2)若
正确答案
见解析。
解析
(1)
因


(2)

当a≥2时,在区间



当0<a<2时,由



∴f(x)的单调减区间为

于是,f(x)在

综上可知,若f(x)得最小值为1,则a的取值范围是
知识点
已知函数


为
(1)求
(2)求函数

正确答案
见解析。
解析
(1)因为
因为函数

所以
(2)由(1)知,函数
当

所以当
当
知识点
已知


正确答案
解析
知识点
设函数
(1)若函数


(2)当b=0时,若不等式

正确答案
见解析。
解析
(1)①
∵函数




②



令



(2)当b=0时,




即


令






(注:也可令




知识点
已知△ABC是边长为3的等边三角形,点D、E分别是边AB、AC上的点,且满足==.将ADE沿DE折起到1ADE的位置,并使得平面A1DE⊥平面BCED.
(1)求证:A1D⊥EC;
(2)设P为线段BC上的一点,试求直线PA1与平面A1BD所成角的正切的最大值。
正确答案
见解析
解析
证明:(1)因为等边△

所以



由余弦定理得
因为
所以
折叠后有
因为平面







故A1D⊥EC.
(2)法一:由(1)的证明,可知


以







作







所以


所以
因为


设直线


所以
①若
②若
令
因为函数

即
所以
故所求的最大值为
法二:如图,
作




由(1)有



所以


所以


设


所以A1H=
所以在


①若x=0,则tan
②若

令



所以tan

知识点
扫码查看完整答案与解析




























































