函数的最值及其几何意义
共151题

· 函数的最值及其几何意义

函数的最值及其几何意义
共151题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

12．定义在R上的函数满足，当时，，则函数在上有（）

A最小值

B最大值

C最小值

D有最大值

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值及其几何意义抽象函数及其应用

题型：简答题

简答题 · 12 分

20．某车间有50名工人，要完成150件产品的生产任务，每件产品由3个型零件和1个型零件配套组成，每个工人每小时能加工5个型零件或者3个型零件，现在把这些工人分成两组同时工作（分组后人数不再进行调整），每组加工同一种型号的零件.设加工型零件的工人人数为名（N）.

（1）设完成、B型零件加工所需时间分别为、小时，写出和的解析式；

（2）为了在最短时间内完成全部生产任务，应取何值，最短时间是多少？

正确答案

（1）生产150件产品，需加工A型零件450个，

则完成A型零件加工所需时间

生产150件产品，需加工型零件150个，

则完成型零件加工所需时间

（2）设完成全部生产任务所需时间为小时，则为与的较大者.

令，即，解得.

所以，当时，；当时，.

故.

当时，，故在上单调递减，

则在上的最小值为（小时）；

当时，，故在上单调递增，

则在上的最小值为（小时）；

，在上的最小值为

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值及其几何意义函数模型的选择与应用

题型：填空题

填空题 · 4 分

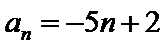
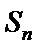
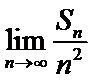
6．已知数列的通项，其前n项和为，则=_______________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值及其几何意义

题型：填空题

填空题 · 4 分

9．某类产品按工艺共分10个档次，最低档次产品每件利润为8元．每提高一个档次，每件利润增加2元。用同样工时，可以生产最低档产品60件，每提高一个档次将少生产3件产品。则获得利润最大时生产产品的档次是________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值及其几何意义二次函数的应用

题型：简答题

简答题 · 12 分

21．已知一家公司生产某种品牌服装的年固定成本为10万元，每生产1千件需另投入2.7万元。设该公司一年内共生产该品牌服装x千件并全部销售完，每千件的销售收入为R（x）万元，且

（1）写出年利润W（万元）关于年产量x（千件）的函数解析式；

（2）年产量为多少千件时，该公司在这一品牌服装的生产中所获得利润最大？

（注：年利润=年销售收入—年总成本）

正确答案

解：（1）当；

（2）①当，

②当时，

综合①②知当时，W取最大值38.6万元，故当年产量为9千件时，该公司在这一品牌服装的生产中所获年利润最大。

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值及其几何意义分段函数模型函数模型的选择与应用

题型：简答题

简答题 · 14 分

20．已知函数有最小值

（1）求实常数的取值范围；

（2）设为定义在上的奇函数，且当时，，求的解析式

正确答案

（1）

所以，当时，有最小值，

（2）由为奇函数，有，得．

当时，

当，则，由为奇函数，得．

所以，

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法函数的最值及其几何意义函数奇偶性的性质

题型：简答题

简答题 · 16 分

22．已知函数．

（1）设，求的取值范围；

（2）关于的方程，，存在这样的值，使得对每一个确定的，方程都有唯一解，求所有满足条件的．

（3）证明：当时，存在正数，使得不等式成立的最小正数，并求此时的最小正数．

正确答案

（1）函数定义域，

，，，即的取值范围是

（2），由（1），，

在单调递增，所以．设，则，

即，即．故，存在，使得对每一个

，方程都有唯一解．

（3）

．

以下证明，对的数及数，

不等式不成立．

反之，由，亦即成立，

因为，，但，这是不可能的．

这说明是满足条件的最小正数．

这样，不等式恒成立，

即恒成立，

∴ ，最小正数=4

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域函数的最值及其几何意义不等式恒成立问题

题型：填空题

填空题 · 4 分

12．已知函数

①；

②；

③；

④，

其中对于在定义域内任意一个值，都存在定义域内唯一的值，使成立，则满足这个条件的函数序号是______________．

正确答案

②

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值及其几何意义余弦函数的定义域和值域

题型：简答题

简答题 · 12 分

17．已知f（x）为定义在[－1，1]上的奇函数，当x∈[－1，0]时，f（x）＝－（a∈R）．

（1）写出f（x）在[0，1]上的解析式；

（2）求f（x）在[0，1]上的最大值。

正确答案

（1）∵f（x）为定义在[－1，1]上的奇函数，

且f（x）在x＝0处有意义，

∴f（0）＝0，即f （0）＝－＝1－a＝0．∴a＝1．

设x∈[0，1]，则－x∈[－1，0]．

∴f（－x）＝－＝4x－2x．

又∵f（－x）＝－f（x）

∴－f（x）＝4x－2x．

∴f（x）＝2x－4x

（2）当x∈[0，1]，f（x）＝2x－4x＝2x－（2x）2，

∴设t＝2x（t>0），

则f（t）＝t－t2．

∵x∈[0，1]，

∴t∈[1，2]．

当t＝1时，取最大值，最大值为1－1＝0．

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法函数的最值及其几何意义函数奇偶性的性质

题型：简答题

简答题 · 12 分

19. 如图，已知三棱柱ABC－A1B1C1的侧棱与底面垂直，AA1＝AB＝AC＝1，AB⊥AC，M是CC1的中点，N是BC的中点，点P在直线A1B1上，且满足．

（1）证明：PN⊥AM．

（2）若平面 PMN与平面ABC所成的二面角为45°，试确定点P的位置．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值及其几何意义

继续学习学习下一知识点

下一知识点 : 奇函数

百度题库 > 高考 > 理科数学 > 函数的最值及其几何意义

扫码查看完整答案与解析