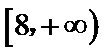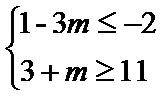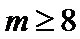- 充要条件的应用
- 共64题
1
题型:
单选题
|
7.设p:实数x,y满足(x–1)2–(y–1)2≤2,q:实数x,y满足
正确答案
A
知识点
充要条件的应用
1
题型:填空题
|
α、β是两个平面,m、n是两条直线,有下列四个命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)
正确答案
②③④
知识点
充要条件的应用空间中直线与直线之间的位置关系空间中直线与平面之间的位置关系
1
题型:填空题
|
14.已知p:﹣2≤x≤11,q:1﹣3m≤x≤3+m(m>0),若¬p是¬q的必要不充分条件,则实数m的取值范围为_______.
正确答案
解析
¬p是¬q的必要不充分条件,
p可推出q,
可得到
解得
考查方向
充分条件、必要条件的判断及其在集合中的应用.
解题思路
本题考查了充分条件、必要条件的判断及其在集合中的应用.充要条件转化之后,用小范围可推出大范围得到结果。
易错点
本题易在充要条件的转化过程中出错
知识点
充要条件的应用
1
题型:填空题
|
13.设命题P:



正确答案

解析
先否定量词,后否定结论,得到的新命题是:

考查方向
本题主要考查了命题的否定、全称量词和存在量词。全称量词和存在量词是新课改增加的内容,需要引起注意。
解题思路
全称命题和特称命题否定的原则是否定量词、否定结论。
易错点
不理解全称命题和特称命题否定的原则而失分。
知识点
充要条件的应用
1
题型:填空题
|
15.下列命题:①已知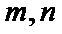
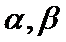
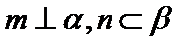
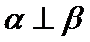
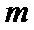
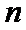
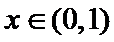
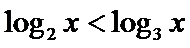
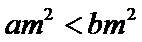
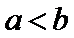
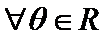
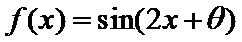
正确答案
①
解析
(1)正确(2)取x=1/2,则不等式不成立,(3)若m为0,则逆命题为假,忽略了等号,(4)当θ=π/2,时,函数为奇函数。所以答案填①
考查方向
直线与平面的位置关系、不等式、简单逻辑
解题思路
根据题意,逐个选项分析
易错点
相关知识点掌握不扎实
知识点
充要条件的应用
下一知识点 : 命题的否定
扫码查看完整答案与解析