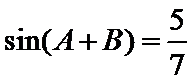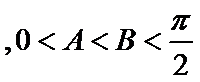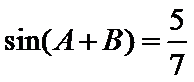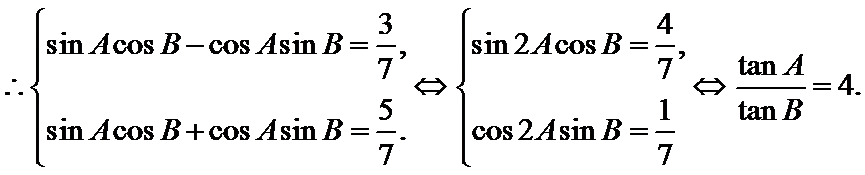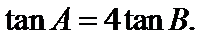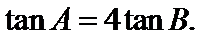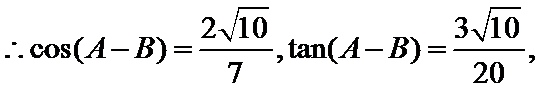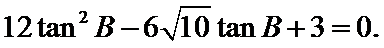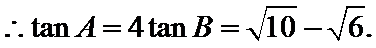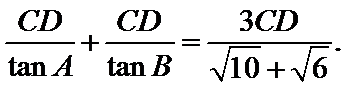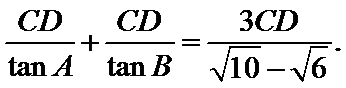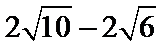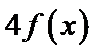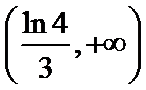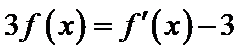- 不等式
- 共1358题
已知点P(x,y)在不等式组

正确答案
答案:-3
解析
可行域是以


知识点
14. 已知变量x,y满足约束条件

正确答案
1
解析
目标函数

考查方向
解题思路
本题属于简单题,
(1)画出约束条件的封闭区域
(2)再
易错点
计算过程易算错x,y满足约束条件的封闭区域
知识点
已知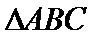
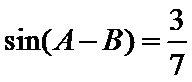
17.求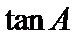
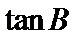
18.若AB=6,求AB边上的高CD
正确答案
(Ⅰ)证明: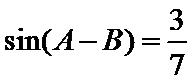
所以
解析
(Ⅰ)证明: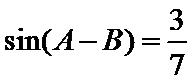
所以
考查方向
解题思路
该题解题思路如下
1)利用两角和差公式 对解析式化简
2)由已知可得到角的范围
易错点
该题对于三角形中的角的关系出错,和角公式展开化简计算错误
正确答案
(II)解: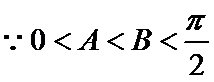
即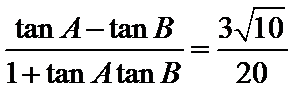
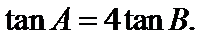
解得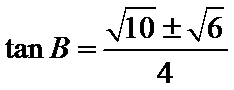
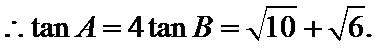
设AB边上的高为CD.
则AB=AD+DB=
或AB=AD+DB=
由AB=6,得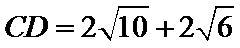
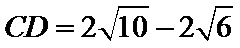
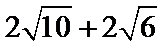
解析
(II)解: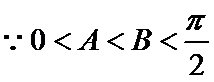
即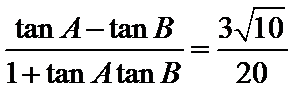
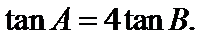
解得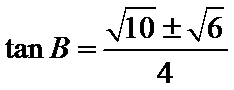
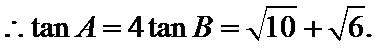
设AB边上的高为CD.
则AB=AD+DB=
或AB=AD+DB=
由AB=6,得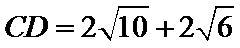
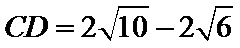
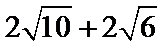
考查方向
解题思路
该题解题思路如下
对解析式解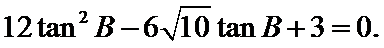
易错点
该题对于三角形中的角与边的关系出错
10.设函数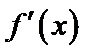

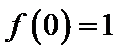
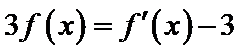
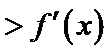
正确答案
解析
:有题意知导函数于原函数之间没有用变量x联系,可知函数与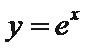
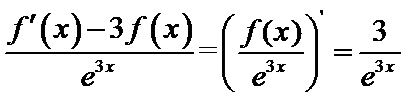
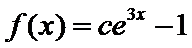
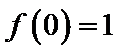
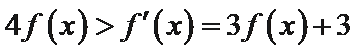
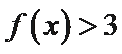
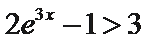

考查方向
解题思路
该题隐含突破点在于
1构造
2根据定积分得原函数函数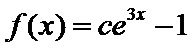
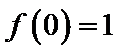
3解指数不等式得出结果
易错点
本题易错于函数的构造过程,
知识点
5.已知实数





正确答案
解析
画出可行域如图
如图可知在C

考查方向
解题思路
该题属于常规题1、画出可行域,注意a的取值2、找出最优解点,并求出点的坐标(含a)3、带入计算
易错点
主要易错于对简单线性规划问题不理解
知识点
正确答案
知识点
正确答案
知识点
5.已知x,y满足约束条件
正确答案
解析
方法1:线性规划问题中最优解出现在可行域的顶点上,因为有三个约束条件,所以顶点即三条直线的交点(两两结合解方程组)A(1,1), B(1,5), C(-3,-3),依次带入判断出答案A,
该方法缺点是只能解决三条直线的问题,超过三条需要判断那些点是在可行域上
方法2:画出可行域如图
考查方向
解题思路
该题有两个解法,方法一:线性规划问题中最优解出现在可行域的顶点上,因为有三个约束条件,所以顶点即三条直线的交点,一一求解验证
方法二,根据条件画出可行域,平移直线3x-2y=0,找出最优解,
易错点
主要体现在两个方面①可行域不规范,②直线平移过程忽略直线的斜率
知识点
8.已知


正确答案
解析
方法1:线性规划问题中最优解出现在可行域的顶点上,因为有三个约束条件,所以顶点即三条直线的交点(两两结合解方程组)A(1,1), B(-2,2), C(-2,-2),依次带入判断出答案C,
该方法缺点是只能解决三条直线的问题,超过三条需要判断那些点是在可行域上
方法2:画出可行域如图当直线过C(-2,-2)点时取得最优解6,选C
考查方向
解题思路
该题有两个解法,方法一:线性规划问题中最优解出现在可行域的顶点上,因为有三个约束条件,所以顶点即三条直线的交点,一一求解验证
方法二,根据条件画出可行域,平移直线
易错点
主要体现在两个方面①可行域不规范,②直线平移过程忽略直线的斜率
知识点
9.若


正确答案
解析







知识点
12.设x,y满足约束条件
正确答案
9
解析
考查方向
解题思路
1、根据不等式组画画出约束条件表示的可行域,并画出函数的图像。
2、平移的图像与区域相交,从而找出最优解,并代入z=x+y得到Z的最大值。
易错点
1、本题易在根据不等式组画平面区域时出错。2、本题容易忽视“Z” 中的几何意义而出错。
知识点
10.函数

正确答案
解析
考查方向
解题思路
1、根据题意构造函数g(x)=xf(x)再得到函数g(x)的单调区间。
2、根据f(x)奇函数判断出g(x)是偶函数,将不等式进行转化,由图象求出不等式成立时x的取值范围即可。
易错点
1、本题由
知识点
13.已知实数x,y满足
正确答案
13
解析
先根据约束条件画出可行域,
而z=x2+y2,表示可行域内点到原点距离OP的平方,
点P在黄色区域里运动时,点P跑到点C时OP最大
当在点C(2,3)时,z最大,最大值为22+32=13,
故答案为:13
考查方向
解题思路
1、根据不等式组画平面区域2、再利用“x2+y2”的几何意义知点C(2,3)到原点距离的平方为x2+y2的最大值。
易错点
1、本题易在根据不等式组画平面区域时出错。2、本题容易忽视“x2+y2”的几何意义为“距离平方”而出错。
知识点
7.若


正确答案
解析
线性目标函数
考查方向
本题主要考察了线性规划,属于中档题,是高考的热点,解决此类题的关键:正确的画出可行域,并理解目标函数的意义。
易错点
1、本题易在画可行域时发生错误
2、本题不容易理解
知识点
15.如果实数


正确答案
25
解析
可行域和初始线如图所示,当平行移动经过点

考查方向
本题主要考查了线性规划求线性目标函数的最值问题,常考的还有斜率型、距离型、函数型。
易错点
作出可行域,还有就是如何衡量最大和最小,忽视则会出现错误。
知识点
扫码查看完整答案与解析