- 不等式
- 共1358题
14.若不等式

正确答案
解析
由题可知SM=2π,SN=48,则P=
考查方向
本题主要考查线性规划及几何概型。
解题思路
解题步骤如下:1、画出平面区域。2、利用概率公式求解.
易错点
本题必须注意利用图像完成。
知识点
15.已知O是坐标原点,点A的坐标为



正确答案
解析
无
考查方向
本题主要考查简单线性规划问题,向量积的运算等考点的理解
解题思路
画出约束直线,然后利用相关概念求解
易错点
线性规划作图时出现错误,向量积运算有误
知识点
9. 已知变量x,y满足条件

正确答案
解析
画出可行域如图所示,
其中B(3,0),C(1,1),D(0,1),
若目标函数z=ax+y仅在点(3,0)处取得最大值,
由图知,

考查方向
本题主要考查简单线性规划的意义及其应用。
解题思路
(1)画出可行区域。
(2)根据已知条件,通过二条直线的斜率关系,求出a的范围.
易错点
(1)不能正确画出可行区域。
(2)不能通过二条直线的斜率关系,找出a的范围。
知识点
6. 设




正确答案
解析
将


当直线















考查方向
解题思路
1.作出


2.由图象判定最优解与最优点;
3.作差,求
易错点
本题易在作可行域时出现错误,易忽视当
知识点
7. 设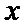
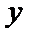

若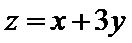
则实数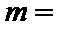
正确答案
解析
首先,作出符合题意的一个可行域如图所示(阴影部分),然后作出目标函数系方程的图像如图可知,当直线经过C(1,2)点时,Z有最大值7;当直线经过A(m-1,m)时Z有最小值:4m-1,由题意可知4m-1=0,即m=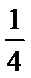
考查方向
解题思路
先假定m值作出可行域,然后作出目标函数直线系方程观测何时取最值,再利用最大值与最小值的差为7建立关于m的方程即可作答。
知识点
15.设




正确答案
解析
由题可知,


考查方向
本题主要考查线性规划及向量的数量积。
解题思路
本题考查线性规划及向量的数量积,解题步骤如下:
1、画出平面区域。
2、化简数量积公式求解.
易错点
本题必须注意利用图像完成。
知识点
15.设实数x,y满足约束条件

正确答案
10
解析
做出题目约束条件表示的可行域,在可行域内部,作出直线,把直线向上平移到约束条件最大,可得最大值为10.
考查方向
简单的线性规划问题.
解题思路
求目标函数的最大值或最小值,必须先求出准确的可行域,令目标函数等于0,将其对应的直线平行移动,最先通过或最后通过的顶点便是最优解
易错点
可行域求解错误
知识点
6.若关于

正确答案
解析
由图可知,当k=0或1时,刚好能构成等腰直角三角形,则面积为

考查方向
本题主要考查线性规划
解题思路
1、表示平面区域;2、求出区域面积,即可得到结果。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在表示平面区域时发生错误。
知识点
16.f(x)是定义在R上的函数,其导函数为f'(x),若f(x)—f'(x) <1,f(0) = 2016,则不等式e x f(x) >e x + 2015(其中e为自然对数的底数)的解集为 .
正确答案
解析
设



考查方向
本题主要考查导数与不等式综合应用
解题思路
构造函数

易错点
如何构造函数,利用函数的单调性求解
知识点
9.若实数


正确答案
解析
画图找到可行域,从图上可以观察出
求解坐标A(1,2) C(1.5,1)
考查方向
解题思路
画图找出可行域,明确目标函数
易错点
无法正确找出可行域以及明白目标函数的意义。
知识点
1. 设

正确答案
解析


知识点
3.设


正确答案
解析
试题分析:作出



考查方向
解题思路
线性目标函数的最优解一般在平面区域的顶点或边界处取得,所以对于一般的求线性目标函数的最值问题,通常可以直接解出可行域的顶点,然后将坐标代入目标函数求出相应的数值,从而确定目标函数的最值.
易错点
对不能准确画出可行域导致出错。
知识点
13.已知函数


正确答案

考查方向
解题思路
对于分段函数的求值问题,一定要注意自变量

由





易错点
本题忽视分段函数的定义域导致错误。
知识点
不等式组

共点,则实数a的取值范围是 .
正确答案
考查方向
易错点
1、本题易在
知识点
12.已知函数



正确答案
1
解析
由上面思路可知


考查方向
解题思路
由函数的图像可知:当0



易错点
不能顺利把不等式问题转化为图像的平移问题,而过份依赖由具体不等式才能解题,对于抽象函数无能为力的思维局限而无法作答出错。
知识点
扫码查看完整答案与解析