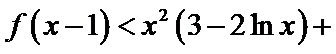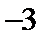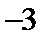- 不等式
- 共1358题
6．若变量
A
B6
C
D4
正确答案
解析
不等式所表示的可行域如下图所
由
考查方向
解题思路
先根据不等式组画出可行域，再找出Z的最小值。
易错点
注意边界线与边界线的交点。
知识点
13.若x，y满足约束条件
正确答案
知识点
2.设变量x，y满足约束条件
A
B6
C10
D17
正确答案
解析
可行域如上图所示，则当取点
考查方向
解题思路
线性规划问题，首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线，其次确定目标函数的几何意义，是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等，最后结合图形确定目标函
易错点
不知道目标函数的几何意义导致本题出错。
知识点
15．若
正确答案
3
解析
作出可行域如图中阴影部分所示，由斜率的意义知，
考查方向
解题思路
本题考查线性规划，具体解题步骤如下：1、由不等式组画可行域。2、由线性目标函数的几何意义得到其最大值。
易错点
1、本题易在画可行域时发生错误2、本题不容易理解
知识点
6.已知
正确答案
解析
做出如图可行域，
当目标函数经过C（4,0）时,截距最大,即
考查方向
解题思路
先根据约束条件画出可行域，再转化目标函数，把求目标函数最值问题转化成求截距的最值问题
易错点
本题易在不等式组表示表示平面区域表示错误
知识点
10.已知R上的奇函数
A
B
C
D
正确答案
解析
设
则
设 
∵
即
则不等式
则x＜1，即不等式
∴所以选项B为正确选项
考查方向
解题思路
构造函数g（x），求函数的导数，判断函数的单调性，利用函数的单调性进行求解即可．
易错点
构造函数g（x）错误
知识点
12.设函数f’(x)是奇函数f (x)(x∈R)的导函数，f（-1）=0，当x>0时，x f’(x)－f (x)＜0，则使得f (x) >0成立的x的取值范围是( )
正确答案
知识点
14.若x，y满足约束条件
正确答案
知识点
4.若变量
正确答案
解析
画出可行域如图三角形所示，由图可知，最优解为A，易知点A(0,1),所以
考查方向
解题思路
先画出可行域，然后将目标函数平移即可得到答案。
易错点
可行域画错导致结果出错。
知识点
7．已知实数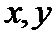
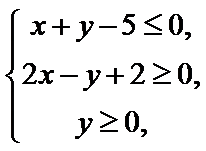
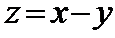
正确答案
解析
由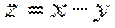
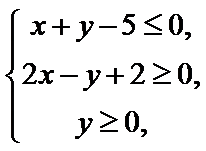
平移直线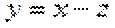
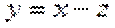
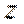
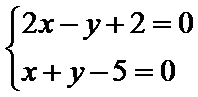
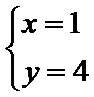
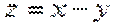
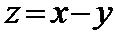
考查方向
解题思路
画出线性约束条件，直接代入区域的顶点坐标，进而比较出最小值即可。
易错点
1、不能准确地画出线性约束条件表示的区域 。2、找最优解时不够准确，弄混最大值和最小值。
知识点
15．设x，y满足约束条件
____________．
正确答案
解析
令x=u,y=
可行域中的点到原点的距离最小值为原点到直线
考查方向
解题思路
先根据条件
易错点
对于条件
知识点
9.若x，y满足
A
B
C
D
正确答案
解析
所求区域如下图，可知B（2，0）点为最大值点，所以kx-y+3=0,代入直线可得2k+3=0,所以k=
考查方向
解题思路
根据已知的约束条件，画出满足约束条件的可行域，再用目标函数的几何意义求解K的值
易错点
可行域区域作图错误，找不到最佳点
知识点
14.若
正确答案
解析
根据约束条件画出可行域
图可知
考查方向
解题思路
该题解题思路
1、题意画出可行域，标记可行域的定点
2、根据 
3、通过旋转移动得出最值
易错点
主要体现在两个方面①可行域不规范，②
知识点
12. 已知实数
则
正确答案
解析
因为点
考查方向
解题思路
易错点
不能正确的画出线性规划可行域，不能正确地识图和用图
知识点
8.已知实数
A
B
C
D
正确答案
解析
由约束条件可知可行域为三角形，且三角形的三个顶点分别为
考查方向
解题思路
1.先根据题中给出的约束条件画出可行域；
2. 将可行域的顶点分别带入目标函数
易错点
1.在画可行域的时候画错；
2.不会转化题中的目标函数
知识点
扫码查看完整答案与解析