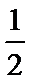- 不等式
- 共1358题
12．设实数
正确答案
8
解析
将
考查方向
解题思路
1)作可行域和目标函数基准直线；
2)平移直线确定最优解；
3)联立方程，求最优解.
易错点
本题易在作可行域时出现错误，易忽视“平面区域的判定方法”.
知识点
14.若
正确答案
5
解析
由已知x,y满足的不等式组所表示的可行域如图所示
所以在点A处时
考查方向
解题思路
首先画出不等式组表示的可行域，
易错点
不等式所表示的平面区域易出错，导致可行域出错。
知识点
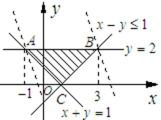
15．设x，y满足不等式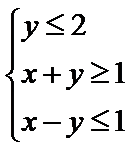
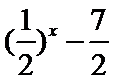
正确答案
解析
作出满足不等式的平面区域，如图所示，当直线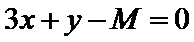
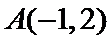
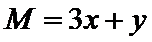
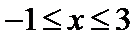
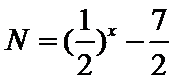
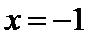
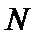
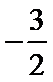
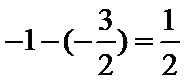
考查方向
解题思路
先作出可行域，再分别求出M,N的最值并确定取得最值的x的值是否相同。
易错点
当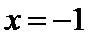
知识点
8．若
A
B
C5
D4
正确答案
解析
将
考查方向
解题思路
1)作出
2） 由图象判定最优解与最优点；
3） 再加绝对值.
易错点
本题易在求目标函数的最值时出现问题，忘记加对值。
知识点
8．设
A
B2
C
D
正确答案
解析
将
考查方向
解题思路
1)作出
2)由图象判定最优解与最优点；
3)再代入
易错点
本题易在求目标函数的最值时出现问题，注意目标函数的斜率与区域边界线的斜率比较
知识点
15．已知x，y满足
正确答案
5
解析
画出可行域如图
如图可知在A
考查方向
解题思路
该题属于常规题
1）画出可行域，注意m的取值
2）找出最优解点，并求出点的坐标（含m）
3）带入计算
易错点
主要易错于对简单线性规划问题不理解
知识点
7.已知
A
B
C0
D1
正确答案
解析
根据约束条件画出可行域
由图 可知在点A（2，2）处取得最值 即z=6-5=1 选D
考查方向
解题思路
该题解题思路
1）题意画出可行域，标记可行域的顶点
2）根据 
3）通过简单的线性规划问题最优解的性质得出最值
易错点
主要体现在两个方面①可行域不规范，②目标函数转化错误
知识点
5. 已知变量
A
B
C
D
正确答案
解析
由约束条件表示的可行域如图所示，作直线l：ax＋y＝0，过点(1，1)作l的平行线l′，则直线l′介于直线x＋2y－3＝0与直线y＝1之间，
因此，－＜－a＜0，即0＜a＜.
考查方向
解题思路
1.先作出可行域； 2. 作直线l：ax＋y＝0，过点(1，1)作l的平行线l′，则直线l′介于直线x＋2y－3＝0与直线y＝1之间，即可得到答案。
易错点
1.可行域画错； 2.不会将题中给出的条件目标函数
知识点
3．若实数
A
B
C
D
正确答案
解析
由
考查方向
解题思路
1.先做出约束条件对应的可行域；2.求出可行域端点的坐标，将目标函数化简为斜截式后平移到点过A点时z最小。
易错点
1.可行域画错；2.误认为直线经过（1，0）时，目标函数取到最小值。
知识点
15.已知点
正确答案
解析
与点M（-1，0）的距离的平方，由图知：
M到直线
由于
考查方向
解题思路
1.先根据题中给出的约束条件画出可行域；2. 
易错点
1.在画可行域的时候画错；
2.不会转化题中的目标函数
知识点
2.已知实数
A-2
B-1
C1
D
正确答案
解析
画出可行域，如图，根据目标函数的斜率为
考查方向
解题思路
画出可行域，根据图形解出目标函数的最大值
易错点
可行域画错，目标函数的处理错误。
知识点
12．不等式组
共点，则实数a的取值范围是 ．
正确答案
解析
作可行域如图所示，直线 y＝a（x＋1）过点 A（－1，0）
且该直线过图中B 点时为临界条件，并且当其斜率小于AB 斜率时均与区域D 有公共点．
B点坐标由x－y＝0和2x＋y－9＝0联立得B（3，3）
．
故a 的取值范围为
考查方向
解题思路
根据不等式组画平面区域，并找出（-1，0）点。过（-1，0）点转动直线与可行域有交点时找出最优解，从而得到
易错点
本题易在
知识点
6．已知实数
正确答案
考查方向
易错点
1、画可行域时易出错；
知识点
9．设不等式组
A
B
C
D
正确答案
考查方向
易错点
1、画可行域时易出错；
知识点
14．x，y满足约束条件
正确答案
知识点
扫码查看完整答案与解析