- 不等式
- 共1358题
13.下列命题为真的是______。
①
②
③
④当x≥2时,
⑤当0<x≤2时,
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
13.已知


正确答案
18
解析
解析已在路上飞奔,马上就到!
知识点
11.受2008年国际金融危机的影响,某企业单位在人事制度改革中对员工进行分流,被分流的入员当年可在原单位领取原工资的100%,从第二年起每年只在原单位领取前一年工资的



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
7.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.因发生意外交通事故,一辆货车上的某种液体泄露到一鱼塘中。为治理污染,根据环保部门的建议,现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂。已知每投放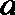
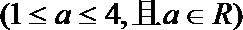
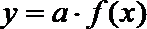
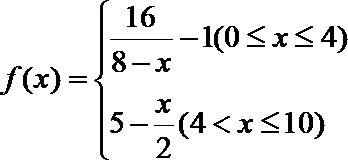
(1)若一次投放4个单位的药剂,则有效治污的时间可达几天?
(2)若因材料紧张,第一次只能投放2个单位的药剂,6天后再投放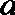
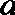
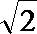
正确答案
(1)因为 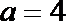
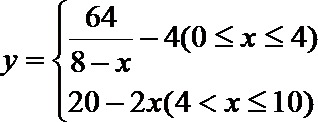
①当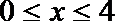
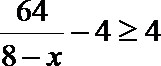
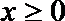
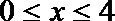
②当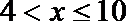
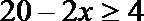
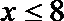
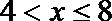
综合得,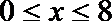
(2) 当
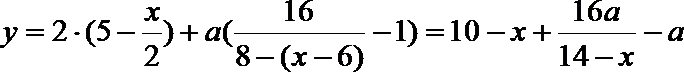
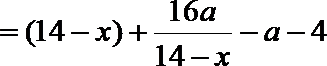
由题意知,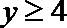
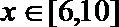
因为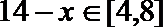
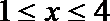
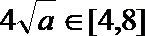
故当且仅当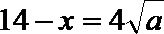
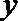

令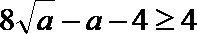
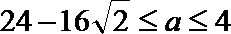
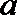
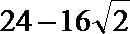
又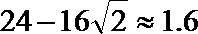
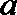
解析
解析已在路上飞奔,马上就到!
知识点
17.某人准备购置一块占地



(1)试用

(2)若要使

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知各项均为正数的等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 函数y=3x2+
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知





正确答案
若

解析
解析已在路上飞奔,马上就到!
知识点
12.已知二次函数


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
10.设



正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点

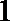
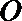
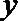
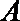
钝角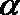
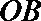
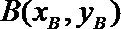
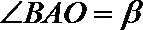
(1)用
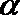
(2)如果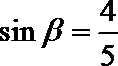
(3)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.为了研究某种药物,用小白鼠进行试验,发现药物在血液内的浓度与时间的关系因使用方式的不同而不同。若使用注射方式给药,则在注射后的3小时内,药物在白鼠血液内的浓度




(1)若a=1,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值?
(2)若使小白鼠在用药后3小时内血液中的药物浓度不低于4,求正数a的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知关于



正确答案
解析
解析已在路上飞奔,马上就到!
知识点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析