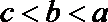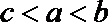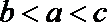- 不等式
- 共1358题
22.证明不等式:
正确答案
即
又

即
解析
解析已在路上飞奔,马上就到!
知识点
9.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分。
22.选修4-1:几何证明选讲
已知









(1)证明:
(2)若

23.选修4-4:坐标系与参数方程
极坐标系与直角坐标系












(I)求证:
(II)当



24.选修4—5:不等式选讲
设函数
(1)求不等式
(2)若存在x使不等式
正确答案
22.(1)∵ PA是切线,AB是弦,∴ ∠BAP=∠C,
又 ∵ ∠APD=∠CPE,
∴ ∠BAP+∠APD=∠C+∠CPE,
∵ ∠ADE=∠BAP+∠APD,∠AED=∠C+∠CPE,
∴ ∠ADE=∠AED.
(2)由(1)知∠BAP=∠C,又 ∵ ∠APC=∠BPA,
∴ △APC∽△BPA, ∴
∵ AC=AP, ∴ ∠APC=∠C=∠BAP,
由三角形内角和定理可知,∠APC+∠C+∠CAP=180°,
∵ BC是圆O的直径,∴ ∠BAC=90°,
∴ ∠APC+∠C+∠BAP=180°-90°=90°, ∠C=∠APC=∠BAP=
在Rt△ABC中,



23.
24.(1)
当


当

当

综上不等式的解集为
(2)
当


当

综上,
另解:画出

解析
解析已在路上飞奔,马上就到!
知识点
5.整数




正确答案
{-1,0,1,2,3}
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知实数x,y满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若
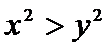
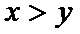
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知二次函数






(Ⅰ)求数列
(Ⅱ)若

(Ⅲ)已知不等式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
从22、23、24题中任选一题作答
22.选修4﹣1几何证明选讲
已知△ABC中AB=AC,D为△ABC外接圆劣弧,
(I)求证.∠CDF=∠EDF
(II)求证:AB•AC•DF=AD•FC•FB.
23.选修4﹣4坐标系与参数方程
在平面直角坐标系中,取原点为极点x轴正半轴为极轴建立极坐标系,已知曲线C1的极坐标方程为:ρ=2cosθ,直线C2的参数方程为:
(I )求曲线C1的直角坐标方程,曲线C2的普通方程.
(II)先将曲线C1上所有的点向左平移1个单位长度,再把图象上所有点的横坐标伸长到原来的
24.选修4﹣5不等式选讲
解不等式:
正确答案
22.证明:(I)∵A,B,C,D 四点共圆,∴∠ABC=∠CDF
又AB=AC∴∠ABC=∠ACB,
且∠ADB=∠ACB,∴∠ADB=∠CDF,7分
对顶角∠EDF=∠ADB,故∠EDF=∠CDF;
(II)由(I)得∠ADB=∠ABF
∵∠BAD=∠FAB
∴△BAD∽△FAB
∴
∴AB2=AD•AF
∵AB=AC
∴AB•AC=AD•AF
∴AB•AC•DF=AD•AF•DF
根据割线定理DF•AF=FC•FB
∴AB•AC•DF=AD•FC•FB
23.(I )C1的极坐标方程为:ρ=2cosθ,即:ρ2=2ρcosθ,
化为直角坐标方程为x2+y2=2x,即为(x﹣1)2+y2=1
直线C2的参数方程为:
消去t得普通方程为x﹣y+4=0
(II)曲线C3上的方程为
设点P(

由三角函数的性质知,
当


所以P点的坐标为(
24.①当x2﹣x<0时,即0<x<1时,不等式成立.
②当x2﹣x>0时,即 x>1 或 x<0时,不等式化为 x2﹣x≥|x|,故有﹣(x2﹣x)≤x≤x2﹣x,
解得 x≥2,或x≤0,
所以,x≥2或x<0.
故原不等式的解集为{x|x≥2或x<0或0<x<1}.
解析
解析已在路上飞奔,马上就到!
知识点
15.设实数



正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
2.设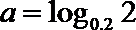
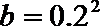
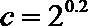
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析