- 不等式
- 共1358题
14. 已知不等式组表示的平面区域为Ω,其中k≥0,则当Ω的面积取得最 小值时的k的值为_______.
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
选做题:请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题计分.
22.选修4—1:几何证明选讲
如图,已知









求证:
(1)
(2)
23.选修4—4:坐标系与参数方程
在直角坐标系







(1)若直线


(2)设


24.选修4—5:不等式选讲
设函数
(1)当
(2)若


正确答案
22.

23.

24.
解析
解析已在路上飞奔,马上就到!
知识点
3.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.不等式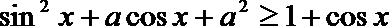
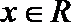
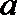
正确答案

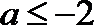
解析
解析已在路上飞奔,马上就到!
知识点
13.变量
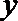
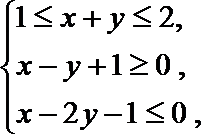
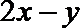
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
6.若实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知


正确答案
-4<m<2
解析
解析已在路上飞奔,马上就到!
知识点
21.设
(Ⅰ) 证明
(Ⅱ) 曲线






(Ⅲ)在第(Ⅱ)问的条件下, 证明
正确答案
解:
(I)设函数

①





②



当




综合①,②及



(II)证明:由(I)知

在区间

因为曲线




且

由
可得


(Ⅲ)设

由

所以
设



故
解析
解析已在路上飞奔,马上就到!
知识点
13.已知实数x、y满足
正确答案
[- 5,7]
解析
解析已在路上飞奔,马上就到!
知识点
15.已知
正确答案
10
解析
解析已在路上飞奔,马上就到!
知识点
7.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.对于实数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若正数x,y满足x+3y=5xy,则3x+4y的最小值是___________
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析















