不等式_章节学习

1

题型：单选题

|

单选题 · 5 分

4．已知，现有下列不等式：

①；

②；

③；

④，

其中正确的是（）

A②④

B①②

C③④

D①③

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用对数值大小的比较不等式的性质利用基本不等式求最值

1

题型：单选题

|

单选题 · 5 分

11.设m,n∈R,定义运算“”和“”如下:

mn=mn=

若正数m,n,a,b满足mn≥4,a+b≤4,则（　　）.

A

B

C

D

正确答案

A

解析

根据题意,知mn表示m,n中的较小的一个,mn表示m,n中较大的一个.

因为4≤mn≤()2,所以m+n≥4.又因为m,n为正数,所以m,n中至少有一个大于或等于2,所以mn≥2.因为a+b≤4,a,b为正数,所以a,b中至少有一个小于或等于2.所以ab≤2.综上所述,知mn≥2,ab≤2,故选A

知识点

不等式的性质进行简单的合情推理

1

题型：单选题

|

单选题 · 3 分

13．如果，那么下列不等式中不正确的是

A

B

C

D

正确答案

B

解析

若a=1,b=2带入验证可得正确选项。A选项不正确，C选项不正确，D选项不正确，所以选B选项。

考查方向

本题主要考查不等式的基本性质

解题思路

本题可依次代入特殊值逐一验证排除。

A选项不正确，C选项不正确，D选项不正确，所以选B选项。

易错点

本题易在代特殊值时发生错误。

知识点

不等式的性质

1

题型：单选题

|

单选题 · 5 分

16．设为实数，则“”是“”的（）

A充分不必要条件

B必要不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

D

解析

（1）若

当时，此时，

即“”“”是假命题

（2）若

当时，此时，

即“”“”是假命题

综上所述，“”是“”的既不充分也不必要条件．故选D

考查方向

本题考查充分条件、必要条件、充分必要条件的判断以及不等式的性质，是容易题，涉及充分必要条件的问题在近几年的各省高考题中出现的频率非常高，它可以与高中数学每一个章节每一个知识点相结合进行命题，是高考的热点问题．

解题思路

根据不等式的性质，先判断“”“”与“”“”的真假，然后结合充分必要条件的定义即可得到答案．判断真命题，需要证明，判断假命题，可以通过举反例的形式来说明．

易错点

对充分性和必要性的认识不足，混淆不等式的各种性质以及各性质需要的前提条件．

知识点

充要条件的判定不等式的性质

1

题型：单选题

|

单选题 · 5 分

8. 我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是：设实数的不足近似值和过剩近似值分别为和（），则是的更为精确的不足近似值或过剩近似值.我们知道，若令，则第一次用“调日法”后得是的更为精确的过剩近似值，即，若每次都取最简分数，那么第四次用“调日法”后可得的近似分数为（）

A

B

C

D

正确答案

A

解析

则第一次用“调日法”后得是的更为精确的过剩近似值，此时；第二次用“调日法”后得是的更为精确的不足近似值，此时；第三次用用“调日法”后得是的更为精确的过剩近似值，；第四次用用“调日法”后得是的更为精确的不足近似值，.从而所得结果为.

B选项不正确，C选项不正确，D选项不正确，所有选A选项.

考查方向

本题主要考查学习应用数学知识的能力，近年来命题频率有所上升.

解题思路

1、按步骤进行计算，逐个得出各次的近似值. 2、计算到第四次的近似值，即可得到结果.

B选项不正确，C选项不正确，D选项不正确，所有选A选项.

易错点

1、本题易把解题的核心问题放有不足近似值和过剩近似值上，使题解复杂化而出错. 2、本题容易在计算化简时出错.

知识点

不等式的性质

1

题型：填空题

|

填空题 · 5 分

12.已知函数则的最小值为．

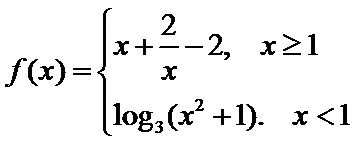
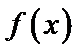
正确答案

1,0

解析

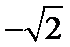
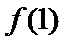
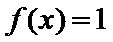
将代入到函数中，得到，所以，因为两个分段函数的函数值都是大于0的，所以函数的最小值为0。

考查方向

分段函数，函数的最值

解题思路

第1问，将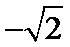代入函数中，进行计算，第2问根据函数取值范围判断

易错点

利用分段函数求函数最值

知识点

不等式的性质

1

题型：单选题

|

单选题 · 5 分

6．设，若，，则p是q的

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分也不必要条件

正确答案

B

解析

由知，而命题，所以，而不能推出，故p是q的必要不充分条件，选择B选项。

考查方向

本题主要考查了充分条件与必要条件的判断,为高考常考题，在近几年的各省高考题出现的频率较高，常与不等式、函数等知识点交汇命题。

解题思路

先由求出的取值范围，再由充分条件与必要条件的定义进行判断。

易错点

解不等式容易出错。

知识点

充要条件的判定不等式的性质

1

题型：单选题

|

单选题 · 5 分

10.设函数在R上存在导数，在上，且，有，则以下大小关系一定正确的是( )

A

B

C

D

正确答案

C

解析

由题可知，f(x)在上是减函数，且，

故。

A选项不正确，B选项不正确，D选项不正确，所以选C选项。

考查方向

本题主要考查了三角函数的基本性质,在近几年的各省高考题出现的频率非常高，常与三角恒等变形公式，函数单调性、周期性、对称型、奇偶性等知识点交汇命题。A选项不正确，B选项不正确，D选项不正确，所以选C选项。

解题思路

本题考查三角函数的性质，解题步骤如下：利用减函数的性质求解即可

易错点

本题易在判断单调性上发生错误。

知识点

函数单调性的判断与证明导数的运算不等式的性质

1

题型：填空题

|

填空题 · 5 分

14.已知实数满足约束条件，则的最小值为 .

正确答案

1

解析

由约束条件确定的可行域如图所示，∴的最小值为．

故此题答案为1。

考查方向

本题主要考查了平面区域的应用,意在考查考生的作图能力以及利用数形结合思想解决问题的能力，在近几年的各省高考题出现的频率较高，常与不等式，直线斜率、坐标轴截距，点到直线距离等知识点交汇命题，此题属于较易题目。

解题思路

1、根据不等式组画平面区域，并画出函数的图像。

2、平移的图像与区域相交，从而找出最优解，并代入得到Z的范围。

易错点

1、本题易在根据不等式组画平面区域时出错。

2、本题容易忽视“Z” 中的几何意义而出错。

知识点

不等式的性质

1

题型：填空题

|

填空题 · 5 分

13. 已知函数，则的值为 .

正确答案

解析

由解析式．

考查方向

本题主要考查了分段函数求函数值.

解题思路

本题考查分段函数求函数值的能力，解题步骤如下：将3代入第二个表达式.2、计算对应的函数值．

易错点

本题必须注意自变量所在对应表达式中的范围，忽视则会出现错误.

知识点

不等式的性质

1

题型：填空题

|

填空题 · 5 分

13．变量，满足条件，求的最大值为_________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

1

题型：填空题

|

填空题 · 5 分

13.已知函数，则 .

正确答案

-2

解析

层层代入可计算出答案。

考查方向

分段函数；函数求值；复合函数

解题思路

根据复合函数性质分层运算

易错点

分段函数分段不成功

知识点

不等式的性质

1

题型：单选题

|

单选题 · 5 分

9．不等式组表示的点集记为M，不等式组表示的点集记为N，在M中任取一点P，则P∈N的概率为（）

A

B

C

D

正确答案

D

解析

解：分别画出点集A，B如图，

A对应的区域面积为4×4=16，B对应的区域面积如图阴影部分面积为：

由几何概型公式得，在A中任取一点P，则P∈B的概率为：

.

故选：D．

考查方向

几何概型和定积分.

解题思路

分别画出点集对应的区域，求出面积，利用几何概型的公式解答.

易错点

画出点集对应的区域，容易出错.

教师点评

本题考查了几何概型的公式的运用；关键是画出区域，求出区域面积，利用几何概型公式求值.

知识点

不等式的性质

1

题型：单选题

|

单选题 · 5 分

2. 设变量满足约束条件，则目标函数的最大值为（）

A0

B3

C6

D12

正确答案

C

解析

画出阴影区域，得端点分别为A(-2，1)，B(-2，7)，C(0，3)。代入求得z的最大值为6.

A选项不正确，B选项不正确，D选项不正确，所以选C选项。

考查方向

本题主要考查了线性规划问题,在近几年的各省高考题出现的频率较高。

解题思路

画出阴影区域，求出端点坐标代入目标函数即可。

易错点

本题易在求端点时发生错误。

知识点

不等式的性质

1

题型：单选题

|

单选题 · 5 分

15．下列四个命题中，为真命题的是（）

A若，则

B若，，则

C若，则

D若，则

正确答案

C

解析

选项A：当时，若，则，故选项A错；

选项B：当时，满足条件，，但，故选项B错；

选项C：若，而，由不等式的传递性可得两边平方，可得，所以，故选项C正确；

选项D：当时，满足条件，但，故选项D错．

考查方向

本题主要考查不等式的基本性质，属于容易题，在近几年的各省高考题中出现的频率较高．

解题思路

对照不等式的八个基本性质，逐项判断每个选项的真假，错误的选项举出反例即可．

易错点

不等式的八个基本性质中每个性质需要的前提条件容易混淆．

知识点

命题的真假判断与应用不等式的性质

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

教师点评

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向