- 不等式
- 共1358题
设变量x,y满足约束条件

正确答案
知识点
20.(本小题满分13分)
已知
(I)讨论
(II)当


正确答案
知识点
9.设直线l1,l2分别是函数f(x)= 
正确答案
知识点
8.若
正确答案
知识点
对于函数f(x),在给定区间[a,b]内任取n+1(n≥2,n∈N*)个数x0,x1,x2,…,xn,使得
a=x0<x1<x2<…<xn-1<xn=b,记S=
22.若函数f(x)=-2x+1,给定区间为[-1,1],求S的值;
23.若函数f(x)=
24.对于给定的实数k,求证:函数f(x)=klnx-
正确答案
(1)4;
解析
(1)解:因为函数f(x)=-2x+1在区间[-1,1]为减函数,
所以f(xi+1)<f(xi),所以|f(xi+1)-f(xi)|= f(xi)-f(xi+1).
S=
=f(x0)-f(xn)=f(-1)-f(1)=4.
考查方向
解题思路
本题考查函数恒成立问题,解题步骤如下:
1)先通过f(x)=-2x+1的单调性,直接求出|f(xi+1)-f(xi)|= f(xi)-f(xi+1)代入即可求出;
易错点
不会转化
正确答案
(2)
解析
(2) 解:由f′(x)=
当x<1时,f′(x)>0,所以f (x)在(-∞,1)为增函数;
当x>1时,f′(x)<0,所以f (x)在(1,+∞)为减函数;
所以f (x)在x=1时取极大值
设xm≤1<xm+1,m∈N,m≤n-1,
则S=
=|f(x1)-f(0)|+…+|f(xm)-f(x m-1)|+|f(xm+1)-f(x m)|+|f(xm+2)-f(x m+1)|+…+|f(2)-f(x n-1)
=[f(x1)-f(0)]+…+[f(xm)-f(x m-1)]+|f(xm+1)-f(x m)|+[f(xm+1)-f(x m+2)]+…+[f(xn-1)-f(2)]
=[f(xm)-f(0)]+|f(xm+1)-f(x m)|+[f(xm+1)-f(2)].
因为|f(xm+1)-f(x m)|≤[f(1)-f(xm)]+[f(1)-f(xm+1)],当x m=1时取等号,
所以S≤f(xm)-f(0)+f(1)-f(xm)+f(1)-f(xm+1)+f(xm+1)-f(2)
=2 f(1)-f(0)-f(2)=
所以S的最大值为
考查方向
解题思路
本题考查函数恒成立问题,解题步骤如下:
2)先研究f(x)=
求出即可;
易错点
不会转化
正确答案
(3)对于给定的实数k,函数f(x)=klnx-
解析
(3)证明:f′(x)=

①当k≥e2时,k-x2≥0恒成立,即f′(x)≥0恒成立,所以f(x)在[1,e]上为增函数,
所以S=
=f(x n)-f(x0)=f(e)-f(1)=k+

因此,存在正数A=k+

②当k≤1时,k-x2≤0恒成立,即f′(x)≤0恒成立,所以f(x)在[1,e]上为减函数,
所以S=
=f(x0)-f(xn)= f(1)-f(e)= 

因此,存在正数A=

③当1<k<e2时,由f′(x)=0,得x=

当f′(x)<0,得


设xm≤
则S=
=|f(x1)-f(x0)|+…+|f(xm)-f(x m-1)|+ |f(xm+1)-f(x m)|+ |f(xm+2)-f(x m+1)|+…+|f(xn)-f(x n-1)
=f(x1)-f(x0)+…+f(xm)-f(x m-1) + |f(xm+1)-f(x m)|+ f(xm+1)-f(x m+2) +…+f(xn-1)-f(x n)
=f(xm)-f(x0) + |f(xm+1)-f(x m)| + f(xm+1)-f(x n)
≤f(xm)-f(x0) + f(xm+1)-f(x n)+ f(

=2 f(




因此,存在正数A=klnk-2k+

综上,对于给定的实数k,函数f(x)=klnx-
考查方向
解题思路
本题考查函数恒成立问题,解题步骤如下:
3)先研究函数f(x)=klnx-
易错点
不会转化
7.若实数


正确答案
解析




考查方向
解题思路
根据


易错点
不会利用基本不等式得到
知识点
4.下面是中国近代出口商品分类比重表(%)。它反映了中国近代经济的哪些特点?( )
①自然经济仍占统治地位
②外国资本在中国占绝对优势地位
③中国经济具有半殖民地经济的特点
④近代工业有了一定的发展
正确答案
解析
此题考查学生对表格信息的提取概括能力。根据材料我们可以看到从1893-1930年,中国近代出口商品中农产品比重不断上升,手工业产品不断下降,机器产品有所上升,说明我国自然经济不断解体,我国近代工业(机器制造业)有所发展,我国被迫卷入资本主义世界市场,半殖民地经济特征日益明显。故正确答案选择C项。
考查方向
解题思路
此题考查学生对表格信息的提取概括能力。根据材料我们可以看到从1893-1930年,中国近代出口商品中农产品比重不断上升,手工业产品不断下降,机器产品有所上升,说明我国自然经济不断解体,我国近代工业(机器制造业)有所发展,我国被迫卷入资本主义世界市场,半殖民地经济特征日益明显。故正确答案选择C项。
易错点
本题易错点在于对材料信息提取不准确
知识点
8.2016年1月18日,蔡英文获得台湾地区领导人选举胜利。美国、德国等多国发表声明说,将维持着一贯的“一个中国”政策,与台湾保持合作关系。下列有关台湾的历史事实阐述正确的是( )
正确答案
解析
此题考查对台海关系史实的认知能力。A项丘逢甲是义军首领,B项德黑兰会议未明确表述,C项朝鲜战争期间美国干涉我国内政,派第七舰队进驻台湾海峡阻止台湾解放,D项《告台湾同胞书》宣布采用和平方式统一祖国的方针,宣布停止炮击金门的命令的是中华人民共和国军事委员会。故正确答案选C项。
考查方向
解题思路
此题考查对台海关系史实的认知能力。A项丘逢甲是义军首领,B项德黑兰会议未明确表述,C项朝鲜战争期间美国干涉我国内政,派第七舰队进驻台湾海峡阻止台湾解放,D项《告台湾同胞书》宣布采用和平方式统一祖国的方针,宣布停止炮击金门的命令的是中华人民共和国军事委员会。故正确答案选C项。
易错点
本题易错点在于误选D项,原因在于对教材细节知识把握不准确。
知识点




正确答案
解析




考查方向
比较大小,定积分.
解题思路
先求定积分,再比较大小。
易错点
定积分求不出来
知识点
15. 下列四个命题中,
为真命题的是( )
正确答案
解析
当


同向不等式有可加性,而同向相减则不一定成立;
如虽然



只有同号不等式才具有可倒性,否则不一定成立。如

因为

考查方向
解题思路
本题考查了不等式的基本性质,适宜于采用排除法求解。
易错点
本题必须注意讨论字母的取值范围,忽视则会出现错误。
知识点
已知



27.求
28.若任意实数



正确答案
见解析
解析



没有递增区间;
考查方向
解题思路
先利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。
易错点
求导数错误,参数的取值范围分类错误
正确答案
见解析
解析
由⑴可知,




令





而


考查方向
解题思路
先利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。
易错点
求导数错误,参数的取值范围分类错误
已知函数


27.求函数
28.当

29.若


正确答案
见解析
解析



考查方向
解题思路
先根据导数的性质求切线的斜率,进而求出参数的值,得到函数的解析式,利用导数的性质作出函数大致图像,结合图像,利用分类讨论思想求K的取值范围.
易错点
求导错误,函数性质理解错误;分类讨论有重有漏
正确答案
见解析
解析
令

当





∴
考查方向
解题思路
先根据导数的性质求切线的斜率,进而求出参数的值,得到函数的解析式,利用导数的性质作出函数大致图像,结合图像,利用分类讨论思想求K的取值范围.
易错点
求导错误,函数性质理解错误;分类讨论有重有漏
正确答案
见解析
解析




令













考查方向
解题思路
先根据导数的性质求切线的斜率,进而求出参数的值,得到函数的解析式,利用导数的性质作出函数大致图像,结合图像,利用分类讨论思想求K的取值范围.
易错点
求导错误,函数性质理解错误;分类讨论有重有漏
已知




20.求

21.记




正确答案
(Ⅰ)
解析
试题分析:本题属于数列的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤进行求解,(2)要注意对
(Ⅰ)设公差为d,
则
由①得

由


所以

考查方向
解题思路
本题考查等差数列、等比数列、裂项抵消法求和,解题步骤如下:
1)设出公差,利用等比中项求公差;
2)利用等差数列的公式得到通项和前
3)利用裂项抵消法进行求解;
4)利用单调性求解。
易错点
1)不能准确裂项;
2)注意数列的单调性的应用.
正确答案
(Ⅱ)
解析
试题分析:本题属于数列的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤进行求解,(2)要注意对
(Ⅱ)可得
所以
由于

因为


所以实数m的取值范围是
考查方向
解题思路
本题考查等差数列、等比数列、裂项抵消法求和,解题步骤如下:
1)设出公差,利用等比中项求公差;
2)利用等差数列的公式得到通项和前
3)利用裂项抵消法进行求解;
4)利用单调性求解。
易错点
1)不能准确裂项;
2)注意数列的单调性的应用.
8.设a,b都是不等于1的正数,则“
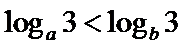
正确答案
解析
若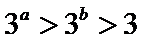
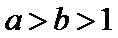
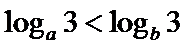
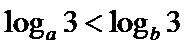
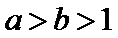
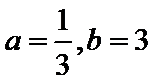
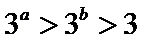
考查方向
解题思路
直接根据充要条件的判断方法判断即可。
易错点
对于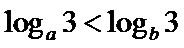
知识点
已知函数
26.若函数

27.若函数

28.若



注:题目中e=2.71828…是自然对数的底数.
正确答案
(Ⅰ)
解析
试题分析:本题属于函数与导数的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤求解,(2)要注意转化思想的应用;
(Ⅰ)



又



则切线l的方程又可表示为
由

考查方向
解题思路
本题考查导数的几何意义和导数的应用,解题步骤如下:
1)求导,利用导数的几何意义求出两曲线的切线方程,利用切线相同进行求解;
2)作差,将问题转化为不等式恒成立问题;
3)构造函数,利用导数研究函数的单调性和最值;
4)利用前一步的结论合理赋值进行求解。
易错点
1)不能正确求导;
2)不能合理转化或赋值.
正确答案
(Ⅱ)
解析
试题分析:本题属于函数与导数的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤求解,(2)要注意转化思想的应用;
a=
(Ⅱ)由题

令



则当x>0时,
由


考查方向
解题思路
本题考查导数的几何意义和导数的应用,解题步骤如下:
1)求导,利用导数的几何意义求出两曲线的切线方程,利用切线相同进行求解;
2)作差,将问题转化为不等式恒成立问题;
3)构造函数,利用导数研究函数的单调性和最值;
4)利用前一步的结论合理赋值进行求解。
易错点
1)不能正确求导;
2)不能合理转化或赋值.
正确答案
(Ⅲ)

解析
试题分析:本题属于函数与导数的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤求解,(2)要注意转化思想的应用;
(Ⅲ)

由题


当


因为


所以
同理
①+②得
因为
由


所以

所以

考查方向
解题思路
本题考查导数的几何意义和导数的应用,解题步骤如下:
1)求导,利用导数的几何意义求出两曲线的切线方程,利用切线相同进行求解;
2)作差,将问题转化为不等式恒成立问题;
3)构造函数,利用导数研究函数的单调性和最值;
4)利用前一步的结论合理赋值进行求解。
易错点
1)不能正确求导;
2)不能合理转化或赋值.
扫码查看完整答案与解析


































