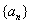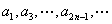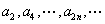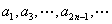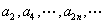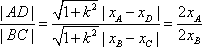- 不等式
- 共1358题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
“

正确答案
解析

但反之不成立,如
知识点
不等式
正确答案

解析
略
知识点
设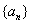
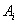

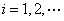
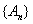
正确答案
解析
由题意知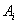
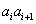
若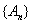
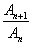
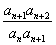
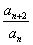
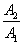
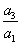
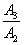
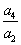
∴
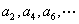
反之,若奇数项和偶数项分别成等比数列,且公比相等,设为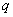
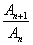
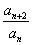
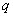
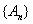
知识点
复数数z满足(z﹣i)(2﹣i)=5.则z=( )
正确答案
解析
(z﹣i)(2﹣i)=5⇒z﹣i=



知识点
在各项均为正数的等比数列



正确答案
4
解析
略
知识点
现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏。
(1)求这4个人中恰有2人去参加甲游戏的概率;
(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(3)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记


正确答案
(1)
(2)
(3)
随机变量

解析
依题意这4个人中,每个人去参加甲游戏的概率为

设“这4个人中恰有


(1) 这4个人中恰有2人去参加甲游戏的概率
(2) 设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B,
则


所以,这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为
(3)



所以
随机变量

知识点
已知函数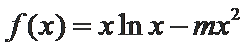
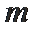
25.当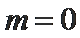
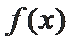
26.若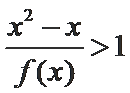
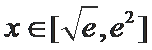
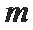
27.若
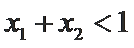
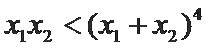
正确答案
当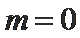
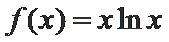
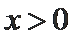
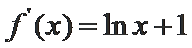
由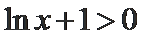
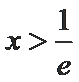
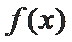
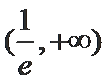
由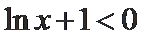
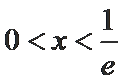
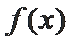
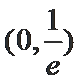
∴综上,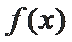
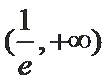
解析
当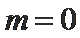
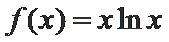
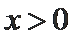
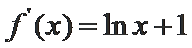
由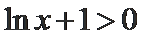
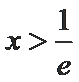
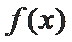
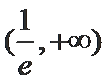
由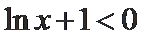
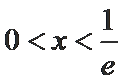
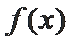
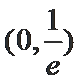
∴综上,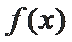
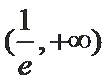
考查方向
本题主要考查了导数的应用——利用导数求函数的单调区间问题,属于常规性问题。
解题思路
首先将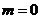
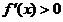
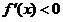
易错点
本题容易因含有对数的超越不等式不会解而导致结果算不出来。
教师点评
本题属于常规性问题,在每一年的高考中都会考到,需要考生加强这一类问题的训练。
正确答案
已知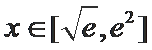
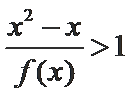
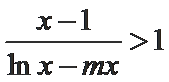
从而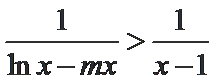
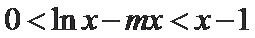
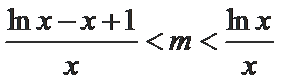
令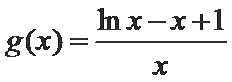
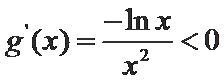
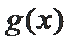
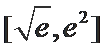
∴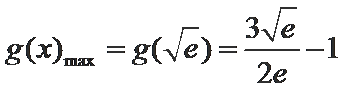
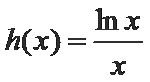
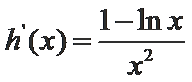
当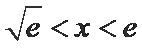
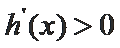
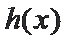
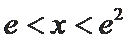
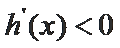
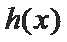
而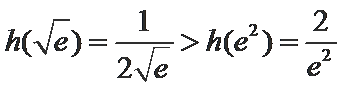
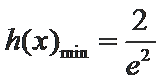
解析
已知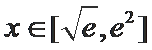
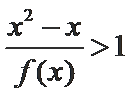
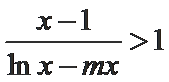
从而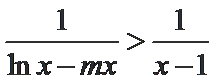
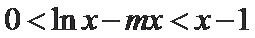
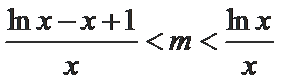
令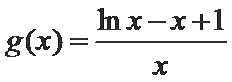
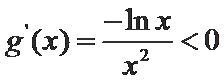
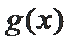
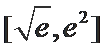
∴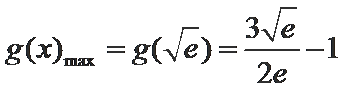
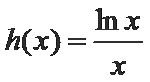
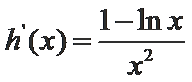
当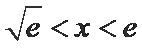
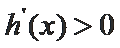
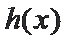
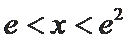
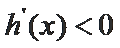
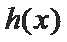
而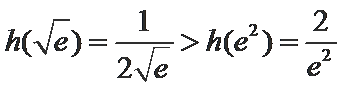
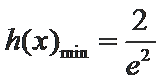
考查方向
本题主要考查了导数的应用,通过求最值来解决不等式恒成立的问题。
解题思路
首先将问题转化为求函数的最值的问题,然后在利用导数予以解决。
易错点
本题在对恒成立问题的分析中容易产生错误的理解而导致出错。
正确答案
由(1)知,当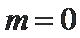
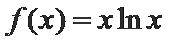
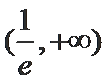
∵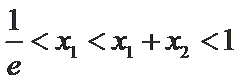
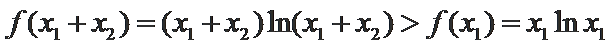
即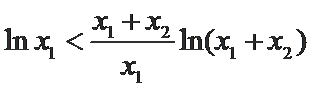
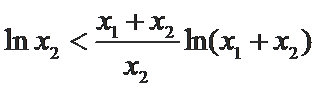
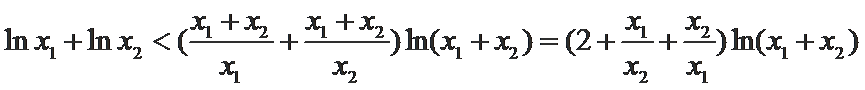
又因为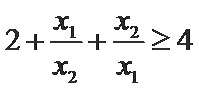
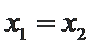
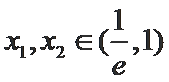
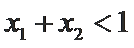
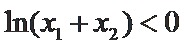
∴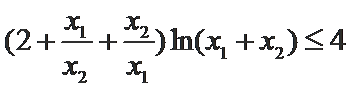
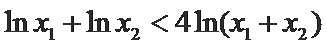
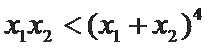
解析
由(1)知,当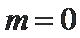
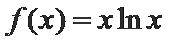
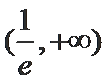
∵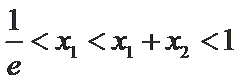
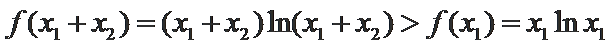
即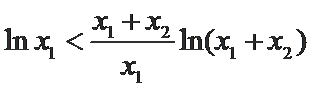
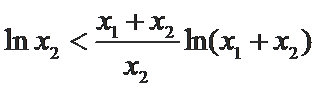
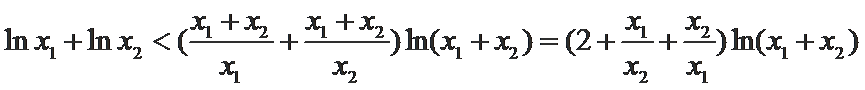
又因为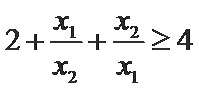
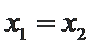
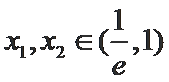
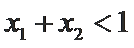
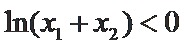
∴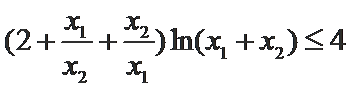
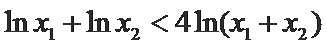
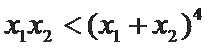
考查方向
本题考查了导数的应用以及不等式的证明。
解题思路
首先根据函数的单调性予以放缩,再利用放缩法予以证明。
易错点
本题容易因为放缩法掌握不清楚而导致出现错误。
教师点评
本题属于不等式的证明问题,难度较大,考生需要有足够的知识储备和应变能力。
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
从n个正整数1,2,…,n中任意取出两个不同的数,若取出的两数之和等于5的概率为
正确答案
8
解析
从1,2,…,n中任取两个不同的数共有


知识点
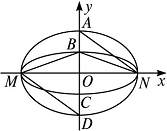
如图,已知椭圆
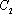

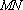

为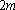
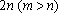

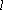
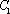
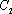
大到小依次为A,B,C,D,记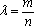
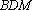
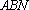
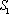
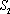
(1)当直线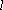
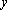
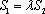
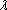
(2)当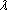
正确答案
(1)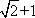

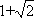
解析
依题意可设椭圆C1和C2的方程分别为
C1: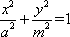
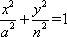
其中a>m>n>0,λ=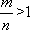
(1)解法1:
如图1,若直线l与y轴重合,即直线l的方程为x=0,则S1=



所以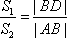
在C1和C2的方程中分别令x=0,可得yA=m,yB=n,yD=-m,
于是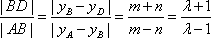
若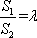
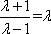
由λ>1,可解得λ=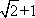
故当直线l与y轴重合时,若S1=λS2,则λ=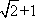
解法2:如图1,若直线l与y轴重合,则
|BD|=|OB|+|OD|=m+n,|AB|=|OA|-|OB|=m-n;
S1=

S2=

所以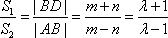
若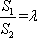
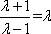
由λ>1,可解得λ=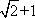
故当直线l与y轴重合时,若S1=λS2,则λ=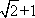
(2)解法1:
如图2,若存在与坐标轴不重合的直线l,使得S1=λS2.根据对称性,不妨设直线l:y=kx(k>0),点M(-a,0),N(a,0)到直线l的距离分别为d1,d2,则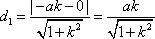
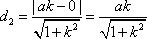
又S1=

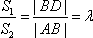
由对称性可知|AB|=|CD|,所以|BC|=|BD|-|AB|=(λ-1)|AB|,
|AD|=|BD|+|AB|=(λ+1)|AB|,于是
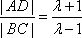
将l的方程分别与C1,C2的方程联立,可求得
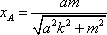
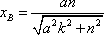
根据对称性可知xC=-xB,xD=-xA,于是
=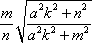
从而由①和②式可得
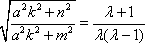
令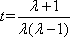
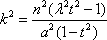
因为k≠0,所以k2>0.于是③式关于k有解,当且仅当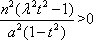
等价于

即
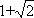
当1<λ≤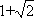
当λ>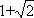
解法2:如图2,若存在与坐标轴不重合的直线l,使得S1=λS2.根据对称性,不妨设直线l:y=kx(k>0),
点M(-a,0),N(a,0)到直线l的距离分别为d1,d2,
则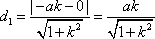
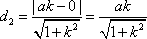
又S1=

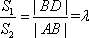
因为
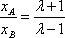
由点A(xA,kxA),B(xB,kxB)分别在C1,C2上,可得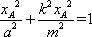
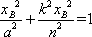
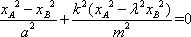
依题意xA>xB>0,所以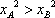
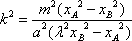
因为k2>0,所以由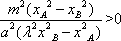
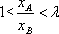
从而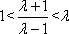
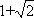
当1<λ≤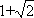
当λ>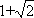
知识点
若实数


正确答案
解析
本题考查了线性规划
作出可行域,因为有最大值,故m>0,联立方程组,得交点为(







知识点
如图,










(1)记平面




(2)设(1)中的直线l与圆











正确答案
见解析
解析
(1)直线l∥平面PAC,证明如下:
连接EF,因为E,F分别是PA,PC的中点,
所以EF∥AC.
又EF

所以EF∥平面ABC.
而EF
因为l

所以直线l∥平面PAC.
(2)
证明:(综合法)如图1,连接BD,由(1)可知交线l即为直线BD,且l∥AC.
因为AB是
所以AC⊥BC,
于是l⊥BC.
已知PC⊥平面ABC,而l
而PC∩BC=C,所以l⊥平面PBC.
连接BE,BF,因为BF
所以l⊥BF.
故∠CBF就是二面角E-l-C的平面角,
即∠CBF=β.
由

连接PQ,DF,因为F是CP的中点,CP=2PF,
所以DQ=PF,
从而四边形DQPF是平行四边形,PQ∥FD.
连接CD,因为PC⊥平面ABC,所以CD是FD在平面ABC内的射影,
故∠CDF就是直线PQ与平面ABC所成的角,即∠CDF=θ.
又BD⊥平面PBC,有BD⊥BF,知∠BDF为锐角,
故∠BDF为异面直线PQ与EF所成的角,即∠BDF=α,
于是在Rt△DCF,Rt△FBD,Rt△BCF中,分别可得
sin θ=


从而sin αsin β=
即sin θ=sin αsin β.
(向量法)如图2,由

图2
连接PQ,EF,BE,BF,BD,由(1)可知交线l即为直线BD.
以点C为原点,向量



于是


所以cos α=

又取平面ABC的一个法向量为m=(0,0,1),可得
设平面BEF的一个法向量为n=(x,y,z),
所以由

于是|cos β|=
从而sin β=
故sin αsin β=
知识点
扫码查看完整答案与解析