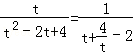- 不等式
- 共1358题
已知函数

(1)求f(x)的最大值和最小值;
(2)若不等式|f(x)﹣m|<2在
正确答案
(1)f(x)max=3,f(x)min=2
(2)(1,4)
解析
(1)∵f(x)=[1﹣cos(

=1+sin2x﹣
=1+2sin(2x﹣
又∵x∈[

∴



∴f(x)max=3,f(x)min=2.…(7分)
(2)∵|f(x)﹣m|<2⇔f(x)﹣2<m<f(x)+2,
∵x∈[

由(1)可知,f(x)max=3,f(x)min=2,
∴m>f(x)max﹣2=1且m<f(x)min+2=4,
∴1<m<4,即m的取值范围是(1,4),…(14分)
知识点
设
正确答案
1
解析


∴
知识点
设变量x,y满足

正确答案
解析
画出可行域,根据图形可知当x=5,y=15时2x+3y最大,最大值为55,故选D
知识点
若
正确答案
解析
设
所以

同理

知识点
已知实数



正确答案
解析
略
知识点
已知函数
(1)当

(2)若f(x)≤2x的解集包含[,1],求
正确答案
见解析
解析
解析:(1)当

①当



②当



③当



……………4分
综上原不等式的解集为
(2)因为f(x)≤2x的解集包含[,1]
不等式可化为|x+a|≤1,………………………………………7分
解得
由已知得
解得
所以

知识点
设函数f(x)=|2x-1|-|x+2|。
(1)解不等式f(x)>0;
(2)若 

正确答案
见解析
解析
(






当






当






综上,不等式

(2)
∴
∵


整理得:

因此m的取值范围是
知识点
不等式组




正确答案
解析
作出不等式组对应的平面区域如图:
若0<a<1,则由图象可知对数函数的图象一定与区域有交点。
若a>1,当对数函数图象经过点A时,满足条件,
此时
解得
∴当1<a≤3时,也满足条件。
∴实数a的取值范围是(0,1)∪(1,3],
故答案为:(0,1)∪(1,3]
知识点
已知Sn=1+



正确答案
m>
解析
由题意,f(n)=S2n+1﹣Sn+1=


∵函数f(n)为增函数,
∴f(n)min=f(2)=
要使对于一切大于1的正整数n,不等式
所以只要

由
此时设[logm(m﹣1)]2=t,则t>0
于是
由此得0<[logm(m﹣1)]2<1
解得m>
知识点
设函数f(x)=|2x+1|-|x-4|。
(1)解不等式:f(x)>0;
(2)若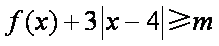
正确答案
(1)x<-5
(2)m≤9
解析
(1)当x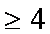
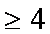
当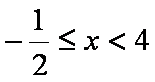
当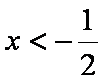
综上,原不等式的解集为{x|x>1或x<-5}。
(2)f(x)+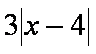
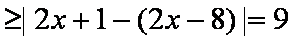
当
知识点
若不等式组


正确答案
解析
略
知识点
关于




正确答案
解析
设



充要条件是













知识点
设函数




(1)求常数
(2)当



(3)求证:对于任意的正整数

正确答案
见解析
解析
(1) 对


(2)由(1)得

① 当









②当









③当








即

综上可知,所求实数


(3) 对要证明的不等式等价变形如下:
对于任意的正整数

对于









对于




取


因此对于任意正整数

知识点
关于x的不等式ax2﹣|x+1|+3a≥0的解集为(﹣∞,+∞),则实数a的取值范围是 。
正确答案
解析
不等式ax2﹣|x+1|+3a≥0,
则a(x2+3)≥|x+1|,
即a≥
设t=x+1,则x=t﹣1,
则不等式a≥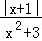
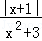
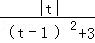
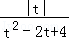
即a>0,
设f(t)=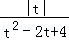
当|t|=0,即x=﹣1时,不等式等价为a+3a=4a≥0,此时满足条件,
当t>0,f(t)=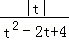
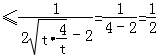
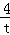
即t=2,即x=1时取等号。
当t<0,f(t)=

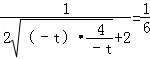
当且仅当﹣t=﹣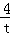
∴t=﹣2,即x=﹣3时取等号。
∴当x=1,即t=2时,fmax(t)=
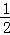
∴要使a≥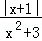
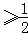
故答案为:[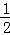
知识点
已知

正确答案
答案:
解析
当


知识点
扫码查看完整答案与解析