· 数列的概念与简单表示法

· 由数列的前几项求通项

由数列的前几项求通项
共778题

· 数列的概念与简单表示法

· 由数列的前几项求通项

由数列的前几项求通项
共778题

热门试卷

X 查看更多试卷

1

题型：简答题

|

简答题 · 14 分

已知数列{}的前n项和 (n为正整数)。

（1）令，求证数列{}是等差数列，并求数列{}的通项公式；

（2）令，试比较与的大小，并予以证明。

正确答案

（1）（2）当，当时.

解析

（1）在中，令n=1，可得，即

当时，，

.

又数列是首项和公差均为1的等差数列

于是

（2）由（1）得，所以

①

②

由①-②得

于是确定的大小关系等价于比较的大小

猜想：当证明如下：

证法1：（1）当n=3时，由猜想显然成立。

（2）假设时猜想成立，即

则时，

所以当时猜想也成立

综合（1）（2）可知，对一切的正整数，都有

证法2：当时

综上所述，当，当时

知识点

由数列的前几项求通项

1

题型：单选题

|

单选题 · 5 分

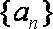
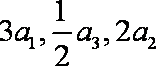
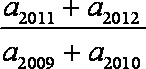
已知正项等比数列中，成等差数列，则=

A3或-1

B9或1

C1

D9

正确答案

D

解析

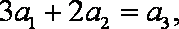
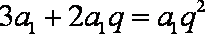
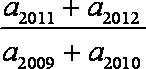
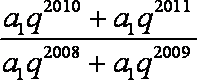
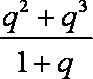
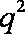
依题意，有即，解得：q＝3

＝＝＝＝9，所以，选D。

知识点

由数列的前几项求通项

1

题型：单选题

|

单选题 · 5 分

在等差数列中，=-2 012 ，其前n项和为，若=2，则的值等于

A-2 011

B-2 012

C-2 010

D-2 013

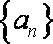
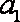
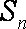
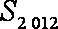
正确答案

B

解析

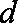
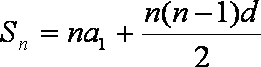
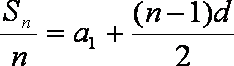
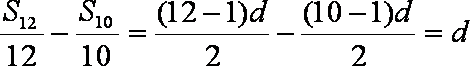
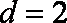
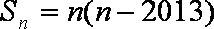
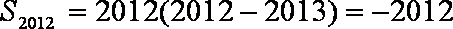
设公差为，则，，由，所以，所以，，选B

知识点

由数列的前几项求通项

1

题型：填空题

|

填空题 · 5 分

设等比数列{}的公比q＝，前n项和为Sn，则＝＿＿＿

正确答案

15

解析

＝＝＝15

知识点

由数列的前几项求通项

1

题型：填空题

|

填空题 · 5 分

设数列{}是公差不为0的等差数列，=1且，，成等比数列，则数列{}的前n项和= 。

正确答案

解析

设公差为d，由，，成等比数列，可得＝1×（1＋5d），解得：d＝，所以Sn＝n＋＝

知识点

由数列的前几项求通项

继续学习学习下一知识点

下一知识点 : 由an与Sn的关系求通项an

百度题库 > 高考 > 理科数学 > 由数列的前几项求通项

扫码查看完整答案与解析