- 由数列的前几项求通项
- 共778题
已知数列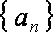
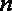
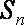
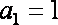
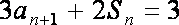
(1)求出数列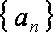
(2)若对任意正整数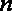
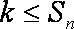
正确答案
见解析。
解析
(1)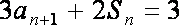
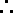

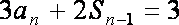
由 ① - ②,得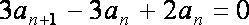
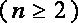
又 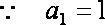
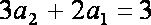
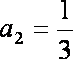
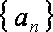
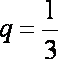
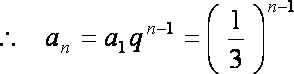
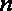
(2)由(Ⅰ)知
由题意可知,对于任意的正整数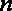

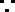

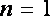

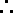
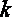
知识点
已知数列{
(1)求数列{
(2)设

(3)设



正确答案
见解析。
解析
(1)由Sn=n2可知,当n=1时,a1=1,
当n≥2时,
所以,
(2)由(1)知:

所以,Tn=



=
(3)由(1)知:

A2=(1+


A3=(1+



从而猜想:

证明如下:
①当n=1时,左边=1+

②假设当n=k时,不等式成立,即

那么Ak+1=(1+




=
这就是说当n=k+1时,不等式成立,
由①②可知,

知识点
等差数列




正确答案
130.
解析
根据等差数列的性质,由
知识点
已知数列{


(1)证明:数列{


(2)若数列{


正确答案
见解析。
解析
证明:(1)由
当n∈N*时,Sn=2an-2n,①
则当n≥2, n∈N*时,Sn-1=2an-1-2(n-1). ②
①-②,得an=2an-2an-1-2,
即an=2an-1+2, ∴an+2=2(an-1+2)
∴
∴ {an+2}是以a1+2为首项,以2为公比的等比数列.
∴an+2=4·2n-1,∴an=2n+1-2,
(2)证明:由



知识点
已知等比数列



(1) 求k的值及数列
(2) 若数列




正确答案
见解析。
解析
解(1) 当n≥2时由


(2) 由






知识点
扫码查看完整答案与解析