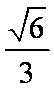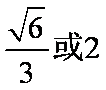- 由数列的前几项求通项
- 共778题
在


正确答案
解析
因为






知识点
有限数列
① 对于任意的


② 对于任意的





(1)若





(2)证明:

(3)求
正确答案
见解析
解析
(1)由①,得
由②,当













经检验,当

(2)假设





由①,
对于数






所以 

(3)

(1)令

(2)设
(ⅰ)
假设






则对









同理:

但

所以 
所以 
(ⅱ)
假设
(ⅲ)
(ⅳ)
综合(ⅰ),(ⅱ),(ⅲ),(ⅳ)可知
………………14分
由(1),(2)可得,
知识点
在各项均为正数的等比数列






正确答案
解析
由



知识点
已知数列{




(I)求证数列{

(2)设


正确答案
见解析。
解析
(1)在


当


∴






于是

(2)∵

∴

由






知识点
已知实数1,m,9成等比数列,则圆锥曲线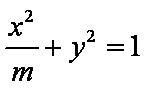
正确答案
解析
根据条件可知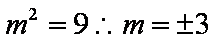
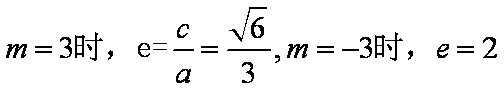
知识点
扫码查看完整答案与解析