- 由数列的前几项求通项
- 共778题
如果数列








(1)已知数列



(2)是否存在一个等差数列是“Ω”数列?请证明你的结论;
(3)如果数列

正确答案
见解析
解析
(1)数列

(2)不存在一个等差数列是“Ω”数列。
证明:假设存在等差数列是“Ω”数列,
则由


所以假设不成立,即不存在等差数列为“Ω”数列。 ……………………7分
(3)将数列
设


任取大于0的一项作为第一项,则满足
假设当
若

若

所以取0或与

如果按上述排列后存在
否则



因为区间

那么从第


综上所述,数列
知识点
已知数列





(1)求出数列
(2)若对任意正整数


正确答案
(1)

解析
解析:(1)



由 ① - ②,得

又 







(2)由(1)知
由题意可知,对于任意的正整数








知识点
已知区域
正确答案
解析
如图,区域M为正方形ABCD,区域N为两个弓形OE与OF的并集。
∴
知识点
已知三个数列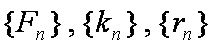
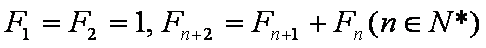
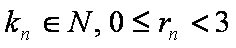
正确答案
解析
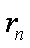
从上面可以看出
r1=1,r3=2,r5=2,r7=1,r9=1,r11=2,r13=2,r15=1
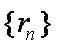
项数共有1006个奇数项,故所求和为
251×6+3=1509 选“D”
知识点
已知数列{an},{bn}满足:a1b1+a2b2+a3b3+…+anbn=

(1)若{bn }是首项为1,公比为2的等比数列,求数列{an}的前n项和Sn;
(2)若{an}是等差数列,且an≠0,问:{bn}是否是等比数列?若是,求{an}和{bn}的通项公式;若不是,请说明理由。
正确答案
见解析。
解析
(1)因为a1b1+a2b2+a3b3+…+anbn=
则

两式相减,得anbn=n·2n(n≥2),
当n=1时,a1b1=2,满足上式,所以anbn=n·2n(nN*),
又因为{bn }是首项为1,公比为2的等比数列,则bn=
故数列{an}是首项为2,公差为2的等差数列,
所以
(2)设{an}的公差为d,则an=a1+(n-1)d,由(1)得
则

故当

当
知识点
扫码查看完整答案与解析