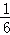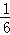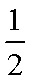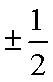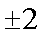- 由数列的前几项求通项
- 共778题
已知等差数列





(1)求数列
(2)令


正确答案
(1)
解析
解析:(1)∵ 数列
∴ 

∴ 

∵ 公差


∴ 

∴ 
(2)∵ 
∴
当且仅当


知识点
设





(1)求证:数列
(2)已知数列
① 求数列

② 是否存在元素均为正整数的集合







正确答案
见解析
解析
(1)证明:依题意,

从而

所以


(2)① 法1:由(1)得,等比数列



则
解得

且
解得

所以

法2:依题意,得
消去
消去
消去

从而可解得,


所以

② 假设存在满足题意的集合








则
因为

若

结合①得,
化简得,
因为


所以只能
同理,
所以




即
故


所以假设不成立,从而不存在满足题意的集合
知识点
数列{an}满足a1=2,an=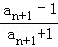
正确答案
解析
∵an=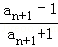
∴an+1=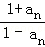
∵a1=2,∴a2=﹣3,a3=﹣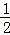
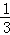
∴数列{an}是周期为4的周期数列,且a1a2a3a4=1,
∵2014=4×503+2,
∴T2014=﹣6。
知识点
已知等差数列


若


正确答案
7
解析
略
知识点
已知等比数列{an}的前n项和为Sn,且满足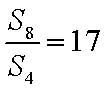
正确答案
解析
由题可知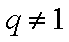
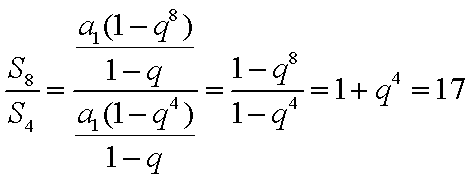
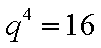
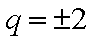
知识点
扫码查看完整答案与解析