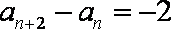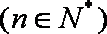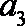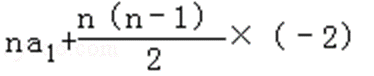由数列的前几项求通项
共778题

· 由数列的前几项求通项

由数列的前几项求通项
共778题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

设实数成等差数列，实数成等比数列，则的取值范围是( )

正确答案

解析

由于实数成等差数列，则；由于实数成等比数列，则，所以，利用基本不等式易得，当同号时，；当异号时，，故选B。

知识点

由数列的前几项求通项

题型：简答题

简答题 · 12 分

已知数列{an}满足：，，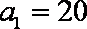

（1）求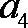，并求数列{an}通项公式；

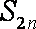
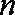
（2）记数列{an}前2n项和为，当取最大值时，求的值。

正确答案

见解析

解析

解析：（1）∵a1=20，a2=7，an+2﹣an=﹣2 ∴a3=18，a4=5

由题意可得数列{an}奇数项、偶数项分布是以﹣2为公差的等差数列

当n为奇数时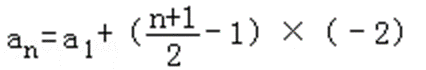，=21﹣n

当n为偶数时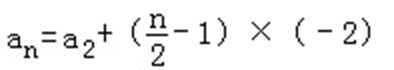，=9﹣n

∴an=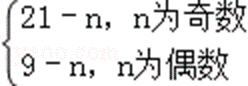---------------------------------------------6分

（2）s2n=a1+a2+…+a2n =（a1+a3+…+a2n﹣1）+（a2+…+a2n）

= =﹣2n2+29n

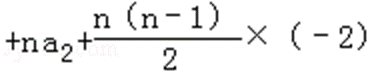
结合二次函数的性质可知，当n=7时最大----------------------------------12分

知识点

由数列的前几项求通项

题型：单选题

单选题 · 5 分

已知函数的定义域为R,且满足：是偶函数，是奇函数，若，则

等于

A-18

B-9

正确答案

解析

由已知得

知识点

由数列的前几项求通项

题型：简答题

简答题 · 12 分

已知等比数列满足：，且是的等差中项。

（1）求数列的通项公式；

（2）若，，求使成立的正整数的最小值。

正确答案

见解析

解析

（1）设等比数列的首项为，公比为，

依题意，有

由①及，得或。

当时，②式不成立；当时，符合题意。

把代入②得，所以，（6分）

（2），

∴，③

，④

③-④得

，（10分）

由成立，得，即。

又当时，；

当时，。

故使成立的正整数的最小值为5.（12分）

知识点

由数列的前几项求通项

题型：填空题

填空题 · 5 分

对于实数，将满足“且为整数”的实数称为实数的小数部分，用符号表示，已知无穷数列满足如下条件：

①；

②。

（1）若时，数列通项公式为；

（2）当时，对任意都有，则的值为。

正确答案

（1）；

（2）或

解析

（1）若时，,则。

（2）当时，由知，，所以，，且。

①当时，，故（舍去）

②当时，，故（舍去）

综上，或

知识点

由数列的前几项求通项

继续学习学习下一知识点

下一知识点 : 由an与Sn的关系求通项an

百度题库 > 高考 > 理科数学 > 由数列的前几项求通项

扫码查看完整答案与解析